Question Number 77186 by jagoll last updated on 04/Jan/20
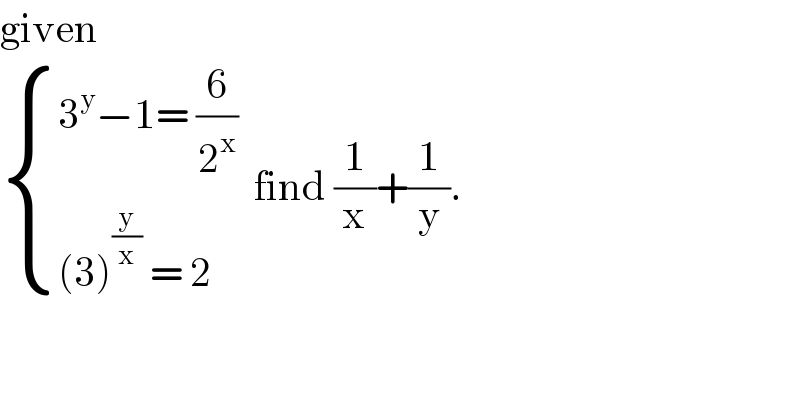
$$\mathrm{given}\: \\ $$$$\begin{cases}{\mathrm{3}^{\mathrm{y}} −\mathrm{1}=\:\frac{\mathrm{6}}{\mathrm{2}^{\mathrm{x}} }}\\{\left(\mathrm{3}\right)^{\frac{\mathrm{y}}{\mathrm{x}}} \:=\:\mathrm{2}\:}\end{cases}\:\:\mathrm{find}\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}. \\ $$
Answered by john santu last updated on 04/Jan/20
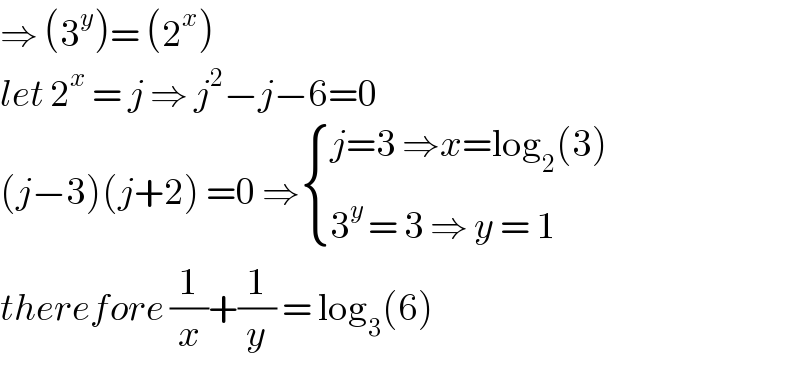
$$\Rightarrow\:\left(\mathrm{3}^{{y}} \right)=\:\left(\mathrm{2}^{{x}} \right) \\ $$$${let}\:\mathrm{2}^{{x}} \:=\:{j}\:\Rightarrow\:{j}^{\mathrm{2}} −{j}−\mathrm{6}=\mathrm{0} \\ $$$$\left({j}−\mathrm{3}\right)\left({j}+\mathrm{2}\right)\:=\mathrm{0}\:\Rightarrow\begin{cases}{{j}=\mathrm{3}\:\Rightarrow{x}=\mathrm{log}_{\mathrm{2}} \left(\mathrm{3}\right)}\\{\mathrm{3}^{{y}\:} =\:\mathrm{3}\:\Rightarrow\:{y}\:=\:\mathrm{1}}\end{cases} \\ $$$${therefore}\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:=\:\mathrm{log}_{\mathrm{3}} \left(\mathrm{6}\right) \\ $$
