Question Number 137584 by bramlexs22 last updated on 04/Apr/21

$${Given}\:\begin{cases}{{a}_{\mathrm{2}{n}} \:=\:{a}_{{n}} .{a}_{\mathrm{2}} \:+\mathrm{1}}\\{{a}_{\mathrm{2}{n}+\mathrm{1}} \:=\:{a}_{{n}} .{a}_{\mathrm{2}} \:−\mathrm{2}\:}\end{cases}\:{and} \\ $$$$\:\begin{cases}{{a}_{\mathrm{7}} \:=\:\mathrm{2}}\\{\mathrm{0}<{a}_{\mathrm{1}} <\mathrm{1}}\end{cases}.\:{Find}\:{a}_{\mathrm{25}} \:=? \\ $$$$ \\ $$
Answered by bemath last updated on 04/Apr/21
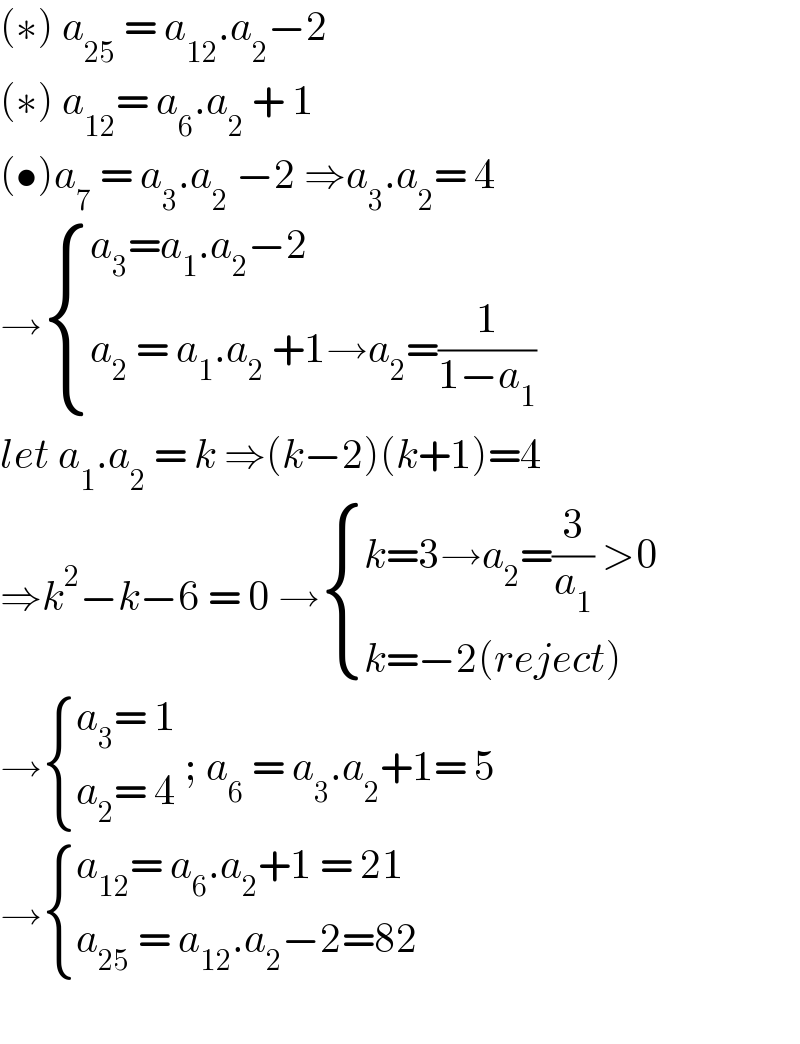
$$\left(\ast\right)\:{a}_{\mathrm{25}} \:=\:{a}_{\mathrm{12}} .{a}_{\mathrm{2}} −\mathrm{2}\: \\ $$$$\left(\ast\right)\:{a}_{\mathrm{12}} =\:{a}_{\mathrm{6}} .{a}_{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$\left(\bullet\right){a}_{\mathrm{7}} \:=\:{a}_{\mathrm{3}} .{a}_{\mathrm{2}} \:−\mathrm{2}\:\Rightarrow{a}_{\mathrm{3}} .{a}_{\mathrm{2}} =\:\mathrm{4} \\ $$$$\rightarrow\begin{cases}{{a}_{\mathrm{3}} ={a}_{\mathrm{1}} .{a}_{\mathrm{2}} −\mathrm{2}}\\{{a}_{\mathrm{2}} \:=\:{a}_{\mathrm{1}} .{a}_{\mathrm{2}} \:+\mathrm{1}\rightarrow{a}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}−{a}_{\mathrm{1}} }}\end{cases} \\ $$$${let}\:{a}_{\mathrm{1}} .{a}_{\mathrm{2}} \:=\:{k}\:\Rightarrow\left({k}−\mathrm{2}\right)\left({k}+\mathrm{1}\right)=\mathrm{4} \\ $$$$\Rightarrow{k}^{\mathrm{2}} −{k}−\mathrm{6}\:=\:\mathrm{0}\:\rightarrow\begin{cases}{{k}=\mathrm{3}\rightarrow{a}_{\mathrm{2}} =\frac{\mathrm{3}}{{a}_{\mathrm{1}} }\:>\mathrm{0}}\\{{k}=−\mathrm{2}\left({reject}\right)}\end{cases} \\ $$$$\rightarrow\begin{cases}{{a}_{\mathrm{3}} =\:\mathrm{1}}\\{{a}_{\mathrm{2}} =\:\mathrm{4}}\end{cases}\:;\:{a}_{\mathrm{6}} \:=\:{a}_{\mathrm{3}} .{a}_{\mathrm{2}} +\mathrm{1}=\:\mathrm{5} \\ $$$$\rightarrow\begin{cases}{{a}_{\mathrm{12}} =\:{a}_{\mathrm{6}} .{a}_{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{21}}\\{{a}_{\mathrm{25}} \:=\:{a}_{\mathrm{12}} .{a}_{\mathrm{2}} −\mathrm{2}=\mathrm{82}\:}\end{cases} \\ $$$$ \\ $$
