Question Number 139254 by mathdanisur last updated on 25/Apr/21
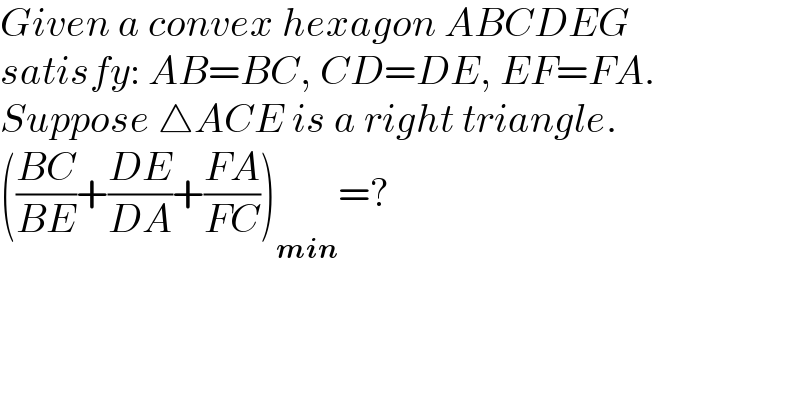
$${Given}\:{a}\:{convex}\:{hexagon}\:{ABCDEG} \\ $$$${satisfy}:\:{AB}={BC},\:{CD}={DE},\:{EF}={FA}. \\ $$$${Suppose}\:\bigtriangleup{ACE}\:{is}\:{a}\:{right}\:{triangle}. \\ $$$$\left(\frac{{BC}}{{BE}}+\frac{{DE}}{{DA}}+\frac{{FA}}{{FC}}\right)_{\boldsymbol{{min}}} =? \\ $$
Answered by mr W last updated on 27/Apr/21

Commented by mr W last updated on 27/Apr/21
![BC=(√(a^2 +p^2 )) BE=(√(a^2 +(2b+p)^2 )) P=((BE)/(BC))=((√(a^2 +(2b+p)^2 ))/( (√(a^2 +p^2 ))))=((√(1+(((2b)/a)+(p/a))^2 ))/( (√(1+((p/a))^2 )))) let x=(p/a), λ=(b/a) P=((√(1+(2λ+x)^2 ))/( (√(1+x^2 )))) (dP/dx)=((2(2λ+x))/(2(√(1+(2λ+x)^2 ))(√(1+x^2 ))))−((2x(√(1+(2λ+x)^2 )))/(2(1+x^2 )(√(1+x^2 ))))=0 (((2λ+x))/( (√(1+(2λ+x)^2 ))))=((x(√(1+(2λ+x)^2 )))/((1+x^2 ))) (1+x^2 )(2λ+x)=x[1+(2λ+x)^2 ] x^2 +2λx−1=0 x=(√(λ^2 +1))−λ=1 for λ=(b/a)=1 P_(max) =((√(1+(2+1)^2 ))/( (√(1+1))))=(√5) (((BC)/(BE)))_(min) =(1/P_(max) )=(1/( (√5))) similarly (((DE)/(DA)))_(min) =(1/( (√5))) with b=a, c=(√2)a FA=(√(c^2 +r^2 )) FC=c+r S=((FA)/(FC))=((√(c^2 +r^2 ))/(c+r))=((√(1+((r/c))^2 ))/(1+(r/c))) y=(r/c) S=((√(1+y^2 ))/(1+y)) (dS/dy)=((2y)/(2(√(1+y^2 ))(1+y)))−((√(1+y^2 ))/((1+y)^2 ))=0 (y/( (√(1+y^2 ))))=((√(1+y^2 ))/(1+y)) y^2 +y=1+y^2 y=1 S_(min) =((√(1+1^2 ))/(1+1))=(1/( (√2))) (((BC)/(BE))+((DE)/(DA))+((FA)/(FC)))_(min) =(1/( (√5)))+(1/( (√5)))+(1/( (√2)))=((2(√2)+(√5))/( (√(10))))](https://www.tinkutara.com/question/Q139475.png)
$${BC}=\sqrt{{a}^{\mathrm{2}} +{p}^{\mathrm{2}} } \\ $$$${BE}=\sqrt{{a}^{\mathrm{2}} +\left(\mathrm{2}{b}+{p}\right)^{\mathrm{2}} } \\ $$$${P}=\frac{{BE}}{{BC}}=\frac{\sqrt{{a}^{\mathrm{2}} +\left(\mathrm{2}{b}+{p}\right)^{\mathrm{2}} }}{\:\sqrt{{a}^{\mathrm{2}} +{p}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{b}}{{a}}+\frac{{p}}{{a}}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\left(\frac{{p}}{{a}}\right)^{\mathrm{2}} }} \\ $$$${let}\:{x}=\frac{{p}}{{a}},\:\lambda=\frac{{b}}{{a}} \\ $$$${P}=\frac{\sqrt{\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\frac{{dP}}{{dx}}=\frac{\mathrm{2}\left(\mathrm{2}\lambda+{x}\right)}{\mathrm{2}\sqrt{\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} }\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}−\frac{\mathrm{2}{x}\sqrt{\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\frac{\left(\mathrm{2}\lambda+{x}\right)}{\:\sqrt{\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} }}=\frac{{x}\sqrt{\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} }}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{2}\lambda+{x}\right)={x}\left[\mathrm{1}+\left(\mathrm{2}\lambda+{x}\right)^{\mathrm{2}} \right] \\ $$$${x}^{\mathrm{2}} +\mathrm{2}\lambda{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}−\lambda=\mathrm{1}\:{for}\:\lambda=\frac{{b}}{{a}}=\mathrm{1} \\ $$$${P}_{{max}} =\frac{\sqrt{\mathrm{1}+\left(\mathrm{2}+\mathrm{1}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\mathrm{1}}}=\sqrt{\mathrm{5}} \\ $$$$\left(\frac{{BC}}{{BE}}\right)_{{min}} =\frac{\mathrm{1}}{{P}_{{max}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${similarly} \\ $$$$\left(\frac{{DE}}{{DA}}\right)_{{min}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${with}\:{b}={a},\:{c}=\sqrt{\mathrm{2}}{a} \\ $$$${FA}=\sqrt{{c}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$${FC}={c}+{r} \\ $$$${S}=\frac{{FA}}{{FC}}=\frac{\sqrt{{c}^{\mathrm{2}} +{r}^{\mathrm{2}} }}{{c}+{r}}=\frac{\sqrt{\mathrm{1}+\left(\frac{{r}}{{c}}\right)^{\mathrm{2}} }}{\mathrm{1}+\frac{{r}}{{c}}} \\ $$$${y}=\frac{{r}}{{c}} \\ $$$${S}=\frac{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{\mathrm{1}+{y}} \\ $$$$\frac{{dS}}{{dy}}=\frac{\mathrm{2}{y}}{\mathrm{2}\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\left(\mathrm{1}+{y}\right)}−\frac{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{{y}}{\:\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{\mathrm{1}+{y}} \\ $$$${y}^{\mathrm{2}} +{y}=\mathrm{1}+{y}^{\mathrm{2}} \\ $$$${y}=\mathrm{1} \\ $$$${S}_{{min}} =\frac{\sqrt{\mathrm{1}+\mathrm{1}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\left(\frac{{BC}}{{BE}}+\frac{{DE}}{{DA}}+\frac{{FA}}{{FC}}\right)_{{min}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{10}}} \\ $$
Commented by mathdanisur last updated on 30/Apr/21

$${thankyou}\:{sir} \\ $$
