Question Number 133994 by benjo_mathlover last updated on 26/Feb/21
![Given a function f satisfies f(x)= { ((x+a(√2) sin x ; 0≤x<(π/4))),((2x cot x +b ; (π/4)≤x≤(π/2))),((a cos 2x−bsin x ; (π/2)<x≤π)) :} continuous in [ 0,π ], then find the value of a and b.](https://www.tinkutara.com/question/Q133994.png)
$$\mathrm{Given}\:\mathrm{a}\:\mathrm{function}\:\mathrm{f}\:\mathrm{satisfies} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{{x}+{a}\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\:;\:\mathrm{0}\leqslant{x}<\frac{\pi}{\mathrm{4}}}\\{\mathrm{2}{x}\:\mathrm{cot}\:{x}\:+{b}\:;\:\frac{\pi}{\mathrm{4}}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}}\\{{a}\:\mathrm{cos}\:\mathrm{2}{x}−{b}\mathrm{sin}\:{x}\:;\:\frac{\pi}{\mathrm{2}}<{x}\leqslant\pi}\end{cases} \\ $$$$\:\mathrm{continuous}\:\mathrm{in}\:\left[\:\mathrm{0},\pi\:\right],\:\mathrm{then}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}\:\mathrm{and}\:{b}.\: \\ $$
Answered by EDWIN88 last updated on 26/Feb/21
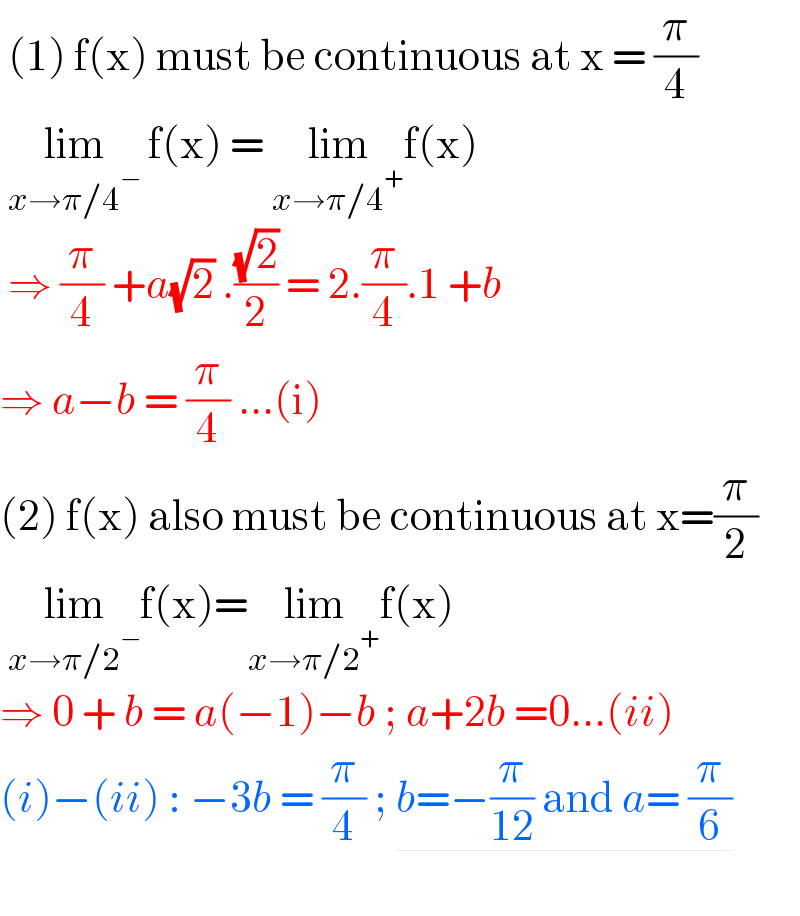
$$\:\left(\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{must}\:\mathrm{be}\:\mathrm{continuous}\:\mathrm{at}\:\mathrm{x}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\:\underset{{x}\rightarrow\pi/\mathrm{4}^{−} } {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\underset{{x}\rightarrow\pi/\mathrm{4}^{+} } {\mathrm{lim}f}\left(\mathrm{x}\right) \\ $$$$\:\Rightarrow\:\frac{\pi}{\mathrm{4}}\:+{a}\sqrt{\mathrm{2}}\:.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:\mathrm{2}.\frac{\pi}{\mathrm{4}}.\mathrm{1}\:+{b}\: \\ $$$$\Rightarrow\:{a}−{b}\:=\:\frac{\pi}{\mathrm{4}}\:…\left(\mathrm{i}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{also}\:\mathrm{must}\:\mathrm{be}\:\mathrm{continuous}\:\mathrm{at}\:\mathrm{x}=\frac{\pi}{\mathrm{2}} \\ $$$$\:\underset{{x}\rightarrow\pi/\mathrm{2}^{−} } {\mathrm{lim}f}\left(\mathrm{x}\right)=\underset{{x}\rightarrow\pi/\mathrm{2}^{+} } {\mathrm{lim}f}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\:\mathrm{0}\:+\:{b}\:=\:{a}\left(−\mathrm{1}\right)−{b}\:;\:{a}+\mathrm{2}{b}\:=\mathrm{0}…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right)\::\:−\mathrm{3}{b}\:=\:\frac{\pi}{\mathrm{4}}\:;\:\underline{{b}=−\frac{\pi}{\mathrm{12}}\:\mathrm{and}\:{a}=\:\frac{\pi}{\mathrm{6}}} \\ $$$$ \\ $$
