Question Number 605 by magmarsenpai last updated on 10/Feb/15
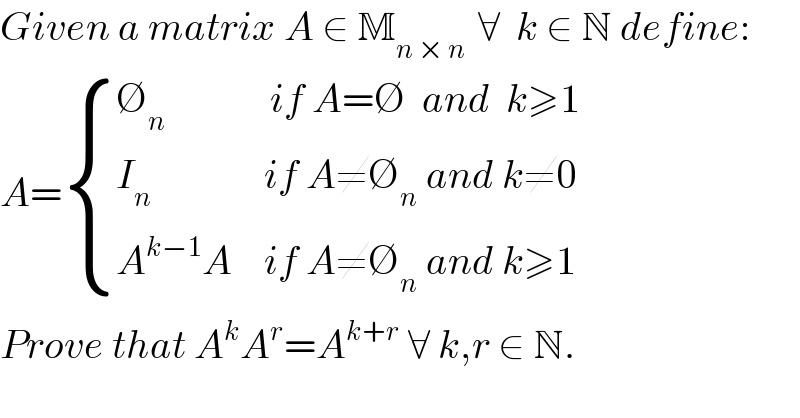
$${Given}\:{a}\:{matrix}\:{A}\:\in\:\mathbb{M}_{{n}\:×\:{n}\:} \:\forall\:\:{k}\:\in\:\mathbb{N}\:{define}: \\ $$$${A}=\begin{cases}{\varnothing_{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{A}=\varnothing\:\:{and}\:\:{k}\geqslant\mathrm{1}}\\{{I}_{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{A}\neq\varnothing_{{n}} \:{and}\:{k}\neq\mathrm{0}}\\{{A}^{{k}−\mathrm{1}} {A}\:\:\:\:{if}\:{A}\neq\varnothing_{{n}} \:{and}\:{k}\geqslant\mathrm{1}}\end{cases} \\ $$$${Prove}\:{that}\:{A}^{{k}} {A}^{{r}} ={A}^{{k}+{r}} \:\forall\:{k},{r}\:\in\:\mathbb{N}. \\ $$
Commented by prakash jain last updated on 09/Feb/15

$$\mathrm{Question}:\:\:{k},\:{r}\in\mathbb{R}\:\mathrm{or}\:{k},{r}\in\mathbb{N}? \\ $$$${A}=\begin{cases}{\varnothing_{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{A}=\varnothing\:\:{and}\:\:{k}\geqslant\mathrm{1}}\\{{I}_{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{A}\neq\varnothing_{{n}} \:{and}\:{k}\neq\mathrm{0}\:\:\:\:\mathrm{check}\:\mathrm{if}\:{k}=\mathrm{0}.}\\{{A}^{{k}−\mathrm{1}} {A}\:\:\:\:{if}\:{A}\neq\varnothing_{{n}} \:{and}\:{k}\geqslant\mathrm{1}}\end{cases} \\ $$$$\mathrm{The}\:\mathrm{definition}\:\mathrm{in}\:\mathrm{line}\:\mathrm{2}\:\mathrm{contradicts}\:\mathrm{with} \\ $$$$\mathrm{definition}\:\mathrm{in}\:\mathrm{line}\:\mathrm{3}. \\ $$$$\mathrm{If}\:{k}\:,\:{r}\:\mathrm{are}\:\mathrm{real}\:\mathrm{then}\:{A}^{{k}} \:\mathrm{needs}\:\mathrm{to}\:\mathrm{be}\:\mathrm{defined} \\ $$$$\mathrm{for}\:{k}<\mathrm{0}.\:{A}^{\mathrm{0}.\mathrm{5}} ={A}^{−\mathrm{0}.\mathrm{5}} {A}=\mathrm{undefined} \\ $$$$\mathrm{If}\:{k},\:{r}\:\mathrm{are}\:\mathrm{postive}\:\mathrm{integers}\:\mathrm{including}\:\mathrm{0}. \\ $$$$\mathrm{The}\:\mathrm{result}\:\mathrm{follows}\:\mathrm{from}\: \\ $$$$\mathrm{property}\:\mathrm{of}\:\mathrm{matrix}\:\mathrm{muliplication}. \\ $$$${A}^{{r}} ={A}\centerdot{A}\centerdot{A}…\left({r}\:\mathrm{times}\right) \\ $$$${A}^{{k}} ={A}\centerdot{A}\centerdot{A}\:…\left({k}\:\mathrm{times}\right) \\ $$
Answered by magmarsenpai last updated on 09/Feb/15
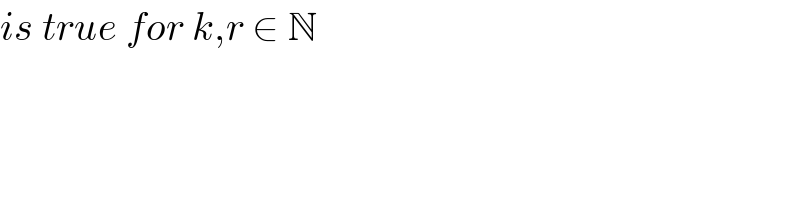
$${is}\:{true}\:{for}\:{k},{r}\:\in\:\mathbb{N} \\ $$
Answered by magmarsenpai last updated on 09/Feb/15
![I solved so : we know : A^k =AA..A (k times) A^r =AA..A (r times) Either: A=(a_(i j) )_(n ×n) ∀ i,j∈{1,...,n} A^k A^r =C=(c_(i j) )_(n x n) we have: c_(i j) =Σ_(j=1) ^n [(a_(i j) )(a_(i j) )..(a_(i j) )][(a_(i j) )(a_(i j) )..(a_(i j) )] c_(i j) =Σ_(j=1) ^n (a_(i j) )^k (a_(i j) )^r =Σ_(j=1) ^n (a_(i j) )^(k+r) ∴ A^k A^r =A^(k+r) , will be well ?](https://www.tinkutara.com/question/Q611.png)
$$\:{I}\:\:{solved}\:{so}\:: \\ $$$${we}\:{know}\:: \\ $$$${A}^{{k}} ={AA}..{A}\:\left({k}\:{times}\right) \\ $$$${A}^{{r}} ={AA}..{A}\:\left({r}\:{times}\right) \\ $$$${Either}:\:{A}=\left({a}_{{i}\:{j}} \right)_{{n}\:×{n}} \:\forall\:{i},{j}\in\left\{\mathrm{1},…,{n}\right\} \\ $$$$\:{A}^{{k}} {A}^{{r}} ={C}=\left({c}_{{i}\:{j}} \right)_{{n}\:{x}\:{n}} \\ $$$${we}\:{have}: \\ $$$${c}_{{i}\:{j}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left[\left({a}_{{i}\:{j}} \right)\left({a}_{{i}\:{j}} \right)..\left({a}_{{i}\:{j}} \right)\right]\left[\left({a}_{{i}\:{j}} \right)\left({a}_{{i}\:{j}} \right)..\left({a}_{{i}\:{j}} \right)\right] \\ $$$${c}_{{i}\:{j}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left({a}_{{i}\:{j}} \right)^{{k}} \left({a}_{{i}\:{j}} \right)^{{r}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\left({a}_{{i}\:{j}} \right)^{{k}+{r}} \\ $$$$\therefore\:{A}^{{k}} {A}^{{r}} ={A}^{{k}+{r}} \:,\:{will}\:{be}\:{well}\:? \\ $$
Answered by prakash jain last updated on 10/Feb/15
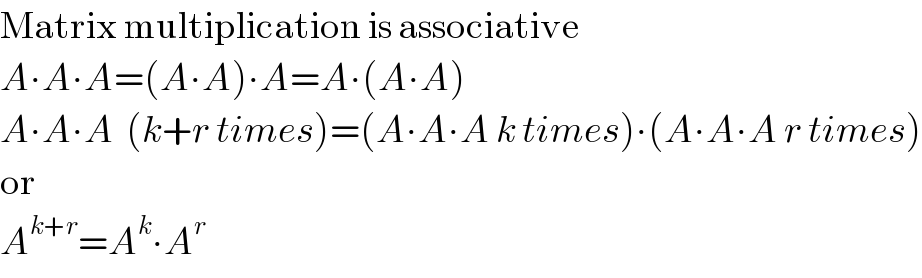
$$\mathrm{Matrix}\:\mathrm{multiplication}\:\mathrm{is}\:\mathrm{associative} \\ $$$${A}\centerdot{A}\centerdot{A}=\left({A}\centerdot{A}\right)\centerdot{A}={A}\centerdot\left({A}\centerdot{A}\right) \\ $$$${A}\centerdot{A}\centerdot{A}\:\:\left({k}+{r}\:{times}\right)=\left({A}\centerdot{A}\centerdot{A}\:{k}\:{times}\right)\centerdot\left({A}\centerdot{A}\centerdot{A}\:{r}\:{times}\right) \\ $$$$\mathrm{or} \\ $$$${A}^{{k}+{r}} ={A}^{{k}} \centerdot{A}^{{r}} \\ $$
