Question Number 77180 by jagoll last updated on 04/Jan/20
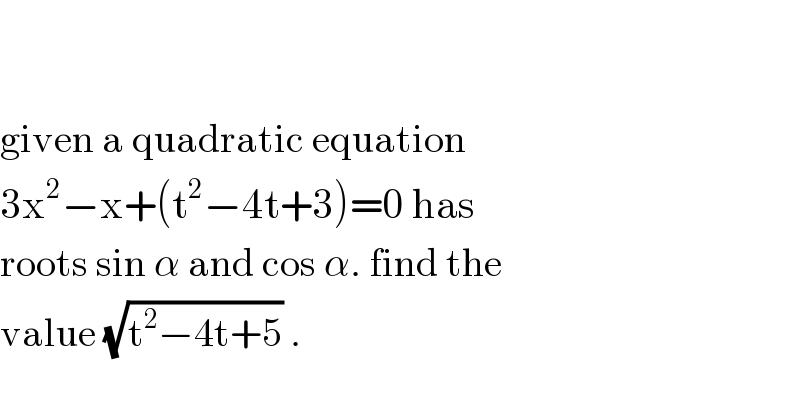
$$ \\ $$$$ \\ $$$$\mathrm{given}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation}\: \\ $$$$\mathrm{3x}^{\mathrm{2}} −\mathrm{x}+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{3}\right)=\mathrm{0}\:\mathrm{has} \\ $$$$\mathrm{roots}\:\mathrm{sin}\:\alpha\:\mathrm{and}\:\mathrm{cos}\:\alpha.\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\mathrm{value}\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{5}}\:. \\ $$
Answered by mr W last updated on 04/Jan/20
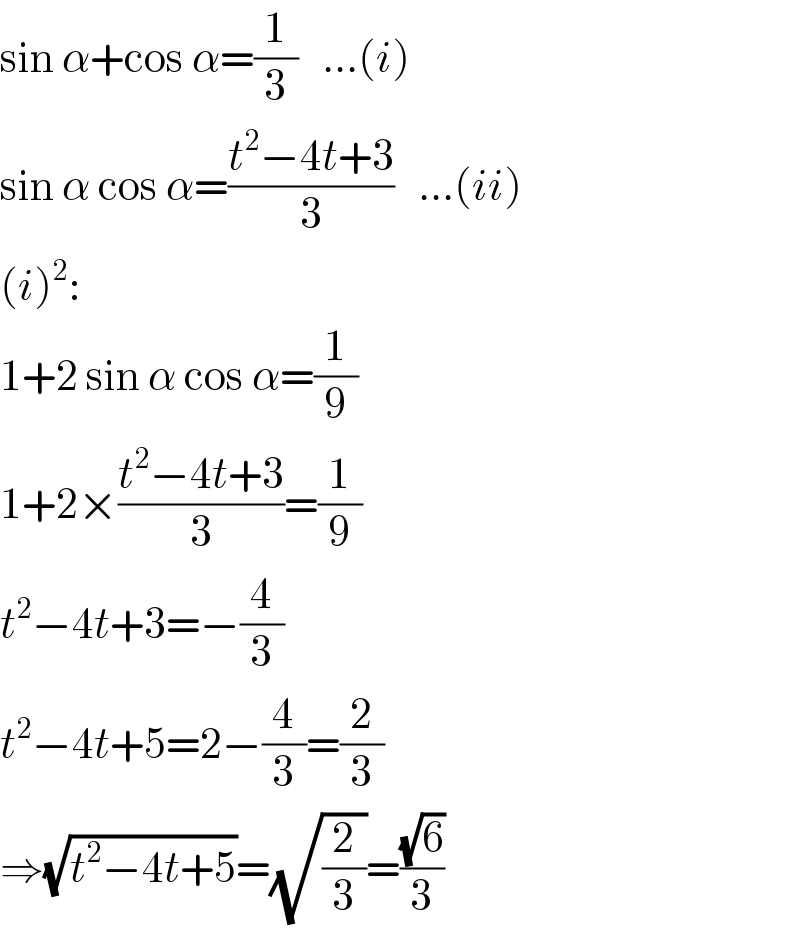
$$\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:…\left({i}\right) \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha=\frac{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{3}}{\mathrm{3}}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} : \\ $$$$\mathrm{1}+\mathrm{2}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{1}+\mathrm{2}×\frac{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{3}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{3}=−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{5}=\mathrm{2}−\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{5}}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}} \\ $$
Commented by jagoll last updated on 04/Jan/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
