Question Number 137338 by liberty last updated on 01/Apr/21
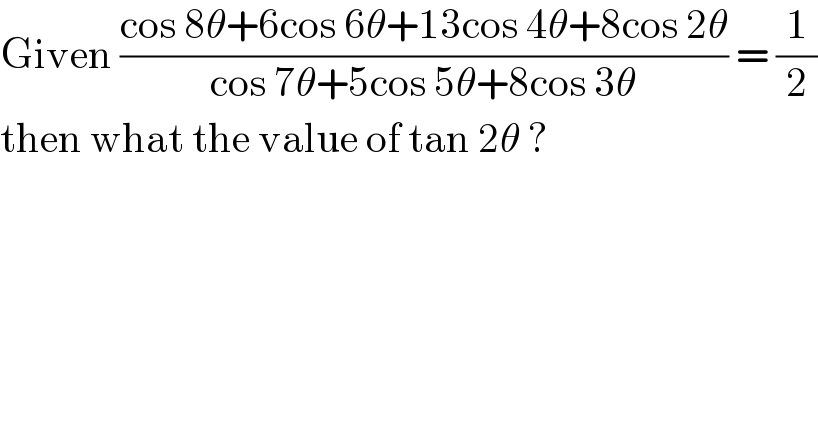
$$\mathrm{Given}\:\frac{\mathrm{cos}\:\mathrm{8}\theta+\mathrm{6cos}\:\mathrm{6}\theta+\mathrm{13cos}\:\mathrm{4}\theta+\mathrm{8cos}\:\mathrm{2}\theta}{\mathrm{cos}\:\mathrm{7}\theta+\mathrm{5cos}\:\mathrm{5}\theta+\mathrm{8cos}\:\mathrm{3}\theta}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{what}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\mathrm{2}\theta\:? \\ $$
Answered by EDWIN88 last updated on 01/Apr/21

$$\mathrm{consider}\:\mathrm{numerator} \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\mathrm{8}\theta+\mathrm{cos}\:\mathrm{6}\theta+\mathrm{5}\left(\mathrm{cos}\:\mathrm{6}\theta+\mathrm{cos}\:\mathrm{4}\theta\right)+\mathrm{8}\left(\mathrm{cos}\:\mathrm{4}\theta+\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$=\:\mathrm{2cos}\:\mathrm{7}\theta\mathrm{cos}\:\theta+\mathrm{5}\left(\mathrm{2cos}\:\mathrm{5}\theta\mathrm{cos}\:\theta\right)+\mathrm{8}\left(\mathrm{2cos}\:\mathrm{3}\theta\mathrm{cos}\:\theta\right) \\ $$$$=\:\mathrm{2cos}\:\theta\left(\mathrm{cos}\:\mathrm{7}\theta+\mathrm{5cos}\:\mathrm{5}\theta+\mathrm{8cos}\:\mathrm{3}\theta\right) \\ $$$$\mathrm{Then}\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{2cos}\:\theta\left(\mathrm{cos}\:\mathrm{7}\theta+\mathrm{5cos}\:\mathrm{5}\theta+\mathrm{8cos}\:\mathrm{3}\theta\right)}{\mathrm{cos}\:\mathrm{7}\theta+\mathrm{5cos}\:\mathrm{5}\theta+\mathrm{8cos}\:\mathrm{3}\theta}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:;\:\mathrm{cos}\:\mathrm{2}\theta\:=\:\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{16}}\right)−\mathrm{1}=−\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$ \mathrm{sin}\:\mathrm{2}\theta=\pm\sqrt{\mathrm{1}−\frac{\mathrm{49}}{\mathrm{64}}}\:=\:\pm\:\frac{\sqrt{\mathrm{15}}}{\mathrm{8}} \\ $$$$ \mathrm{tan}\:\mathrm{2}\theta\:=\:\pm\:\frac{\sqrt{\mathrm{15}}}{\mathrm{7}} \\ $$
