Question Number 135784 by benjo_mathlover last updated on 16/Mar/21
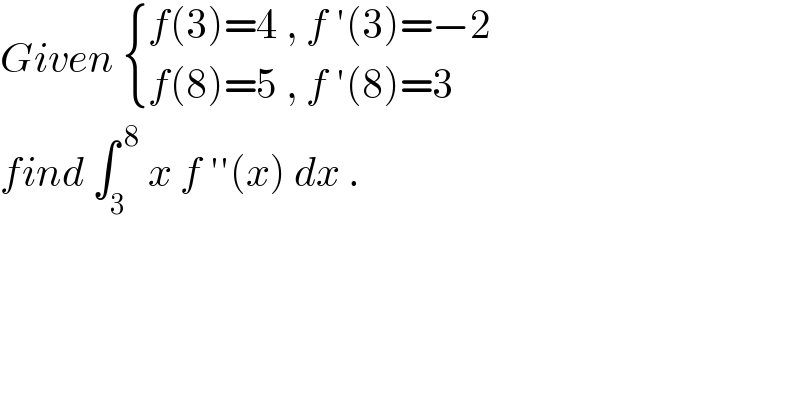
$${Given}\:\begin{cases}{{f}\left(\mathrm{3}\right)=\mathrm{4}\:,\:{f}\:'\left(\mathrm{3}\right)=−\mathrm{2}}\\{{f}\left(\mathrm{8}\right)=\mathrm{5}\:,\:{f}\:'\left(\mathrm{8}\right)=\mathrm{3}}\end{cases} \\ $$$${find}\:\int_{\mathrm{3}} ^{\:\mathrm{8}} \:{x}\:{f}\:''\left({x}\right)\:{dx}\:. \\ $$
Answered by Ar Brandon last updated on 16/Mar/21
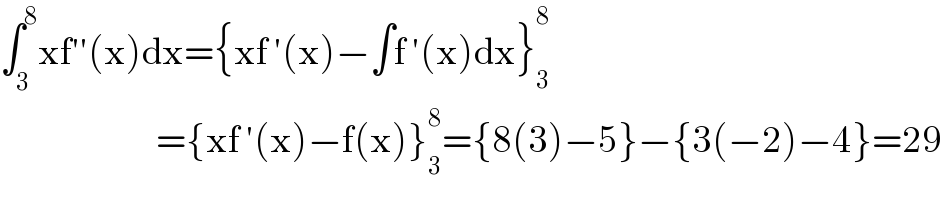
$$\int_{\mathrm{3}} ^{\mathrm{8}} \mathrm{xf}''\left(\mathrm{x}\right)\mathrm{dx}=\left\{\mathrm{xf}\:'\left(\mathrm{x}\right)−\int\mathrm{f}\:'\left(\mathrm{x}\right)\mathrm{dx}\right\}_{\mathrm{3}} ^{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left\{\mathrm{xf}\:'\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{x}\right)\right\}_{\mathrm{3}} ^{\mathrm{8}} =\left\{\mathrm{8}\left(\mathrm{3}\right)−\mathrm{5}\right\}−\left\{\mathrm{3}\left(−\mathrm{2}\right)−\mathrm{4}\right\}=\mathrm{29} \\ $$
