Menu Close

Given-f-x-2-x-2f-x-2-3x-2-9x-2-15x-find-the-value-of-f-2017-

Tinku Tara 0 Comments
Pin




Question Number 137365 by liberty last updated on 02/Apr/21
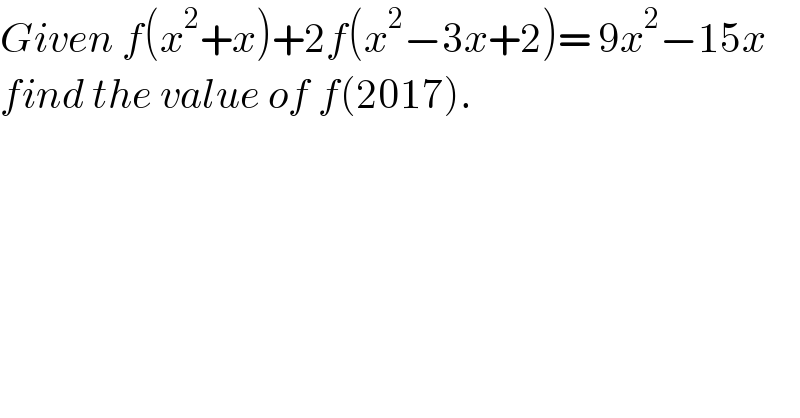
Given f(x^2 +x)+2f(x^2 −3x+2)= 9x^2 −15x find the value of f(2017).
$${Given}\:{f}\left({x}^{\mathrm{2}} +{x}\right)+\mathrm{2}{f}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)=\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{15}{x} \\ $$$${find}\:{the}\:{value}\:{of}\:{f}\left(\mathrm{2017}\right). \\ $$
Answered by MJS_new last updated on 02/Apr/21
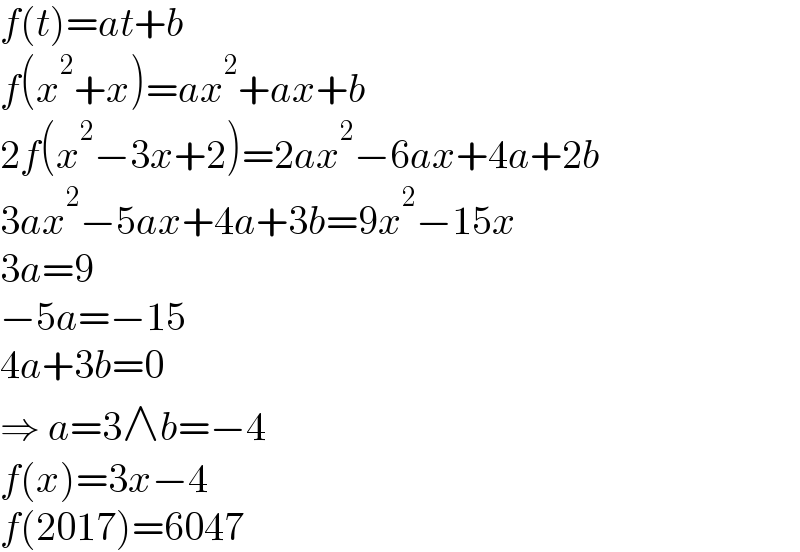
f(t)=at+b f(x^2 +x)=ax^2 +ax+b 2f(x^2 −3x+2)=2ax^2 −6ax+4a+2b 3ax^2 −5ax+4a+3b=9x^2 −15x 3a=9 −5a=−15 4a+3b=0 ⇒ a=3∧b=−4 f(x)=3x−4 f(2017)=6047
$${f}\left({t}\right)={at}+{b} \\ $$$${f}\left({x}^{\mathrm{2}} +{x}\right)={ax}^{\mathrm{2}} +{ax}+{b} \\ $$$$\mathrm{2}{f}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)=\mathrm{2}{ax}^{\mathrm{2}} −\mathrm{6}{ax}+\mathrm{4}{a}+\mathrm{2}{b} \\ $$$$\mathrm{3}{ax}^{\mathrm{2}} −\mathrm{5}{ax}+\mathrm{4}{a}+\mathrm{3}{b}=\mathrm{9}{x}^{\mathrm{2}} −\mathrm{15}{x} \\ $$$$\mathrm{3}{a}=\mathrm{9} \\ $$$$−\mathrm{5}{a}=−\mathrm{15} \\ $$$$\mathrm{4}{a}+\mathrm{3}{b}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\mathrm{3}\wedge{b}=−\mathrm{4} \\ $$$${f}\left({x}\right)=\mathrm{3}{x}−\mathrm{4} \\ $$$${f}\left(\mathrm{2017}\right)=\mathrm{6047} \\ $$
Commented by liberty last updated on 02/Apr/21
thank you
$${thank}\:{you} \\ $$
Answered by EDWIN88 last updated on 02/Apr/21
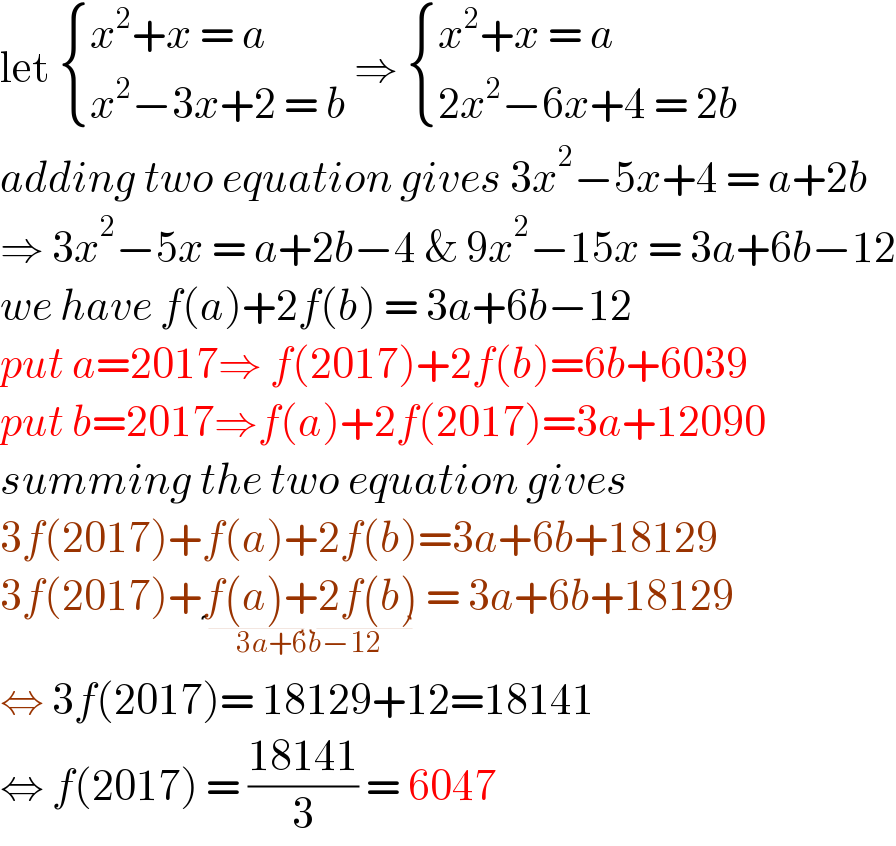
let { ((x^2 +x = a)),((x^2 −3x+2 = b)) :} ⇒ { ((x^2 +x = a)),((2x^2 −6x+4 = 2b)) :} adding two equation gives 3x^2 −5x+4 = a+2b ⇒ 3x^2 −5x = a+2b−4 & 9x^2 −15x = 3a+6b−12 we have f(a)+2f(b) = 3a+6b−12 put a=2017⇒ f(2017)+2f(b)=6b+6039 put b=2017⇒f(a)+2f(2017)=3a+12090 summing the two equation gives 3f(2017)+f(a)+2f(b)=3a+6b+18129 3f(2017)+f(a)+2f(b)_(3a+6b−12) = 3a+6b+18129 ⇔ 3f(2017)= 18129+12=18141 ⇔ f(2017) = ((18141)/3) = 6047
$$\mathrm{let}\:\begin{cases}{{x}^{\mathrm{2}} +{x}\:=\:{a}}\\{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\:=\:{b}}\end{cases}\:\Rightarrow\:\begin{cases}{{x}^{\mathrm{2}} +{x}\:=\:{a}}\\{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{4}\:=\:\mathrm{2}{b}}\end{cases} \\ $$$${adding}\:{two}\:{equation}\:{gives}\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\:=\:{a}+\mathrm{2}{b} \\ $$$$\Rightarrow\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}\:=\:{a}+\mathrm{2}{b}−\mathrm{4}\:\&\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{15}{x}\:=\:\mathrm{3}{a}+\mathrm{6}{b}−\mathrm{12} \\ $$$${we}\:{have}\:{f}\left({a}\right)+\mathrm{2}{f}\left({b}\right)\:=\:\mathrm{3}{a}+\mathrm{6}{b}−\mathrm{12} \\ $$$${put}\:{a}=\mathrm{2017}\Rightarrow\:{f}\left(\mathrm{2017}\right)+\mathrm{2}{f}\left({b}\right)=\mathrm{6}{b}+\mathrm{6039} \\ $$$${put}\:{b}=\mathrm{2017}\Rightarrow{f}\left({a}\right)+\mathrm{2}{f}\left(\mathrm{2017}\right)=\mathrm{3}{a}+\mathrm{12090} \\ $$$${summing}\:{the}\:{two}\:{equation}\:{gives} \\ $$$$\mathrm{3}{f}\left(\mathrm{2017}\right)+{f}\left({a}\right)+\mathrm{2}{f}\left({b}\right)=\mathrm{3}{a}+\mathrm{6}{b}+\mathrm{18129} \\ $$$$\mathrm{3}{f}\left(\mathrm{2017}\right)+\underset{\mathrm{3}{a}+\mathrm{6}{b}−\mathrm{12}} {\underbrace{{f}\left({a}\right)+\mathrm{2}{f}\left({b}\right)}}\:=\:\mathrm{3}{a}+\mathrm{6}{b}+\mathrm{18129} \\ $$$$\Leftrightarrow\:\mathrm{3}{f}\left(\mathrm{2017}\right)=\:\mathrm{18129}+\mathrm{12}=\mathrm{18141} \\ $$$$\Leftrightarrow\:{f}\left(\mathrm{2017}\right)\:=\:\frac{\mathrm{18141}}{\mathrm{3}}\:=\:\mathrm{6047} \\ $$
Commented by liberty last updated on 02/Apr/21
nice
$${nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *