Question Number 133973 by liberty last updated on 26/Feb/21
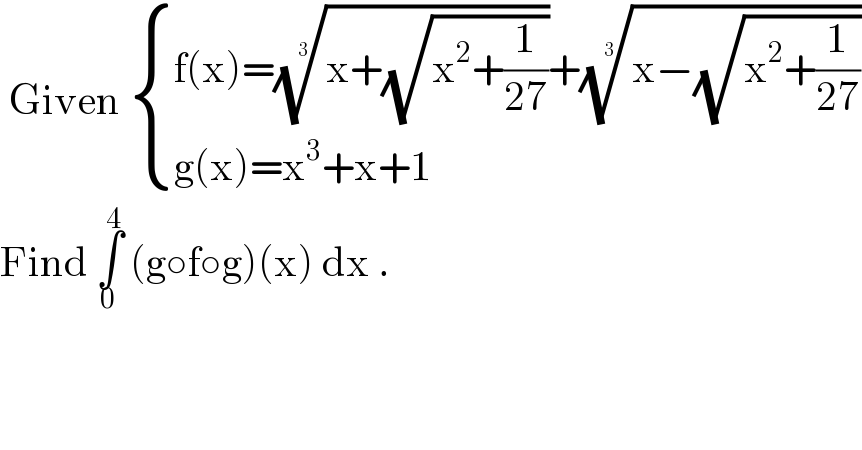
$$\:\mathrm{Given}\:\begin{cases}{\mathrm{f}\left(\mathrm{x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{27}}}}}\\{\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} +\mathrm{x}+\mathrm{1}}\end{cases} \\ $$$$\mathrm{Find}\:\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\:\left(\mathrm{g}\circ\mathrm{f}\circ\mathrm{g}\right)\left(\mathrm{x}\right)\:\mathrm{dx}\:. \\ $$
Answered by EDWIN88 last updated on 26/Feb/21
![recall (a+b)^3 = a^3 +b^3 +3ab(a+b) from f(x)=((x+(√(x^2 +(1/(27))))))^(1/3) +((x−(√(x^2 +(1/(27))))))^(1/3) (f(x))^3 = 2x −f(x) ⇒(f(x))^3 +f(x)= 2x this yields (g○f)(x)= (f(x))^3 +f(x)+1=2x+1 ⇒(g○f○g)(x)= 2g(x)+1=2x^3 +2x+3 then λ = ∫_0 ^4 (2x^3 +2x+3)dx = [ (x^4 /2) + x^2 +3x ]_0 ^4 = 128+16+12 = 156](https://www.tinkutara.com/question/Q133974.png)
$$\:\mathrm{recall}\:\left({a}+{b}\right)^{\mathrm{3}} =\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$\mathrm{from}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{27}}}} \\ $$$$\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{3}} \:=\:\mathrm{2x}\:−\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{3}} +\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{2x} \\ $$$$\mathrm{this}\:\mathrm{yields}\:\left(\mathrm{g}\circ\mathrm{f}\right)\left(\mathrm{x}\right)=\:\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{3}} +\mathrm{f}\left(\mathrm{x}\right)+\mathrm{1}=\mathrm{2x}+\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{g}\circ\mathrm{f}\circ\mathrm{g}\right)\left(\mathrm{x}\right)=\:\mathrm{2g}\left(\mathrm{x}\right)+\mathrm{1}=\mathrm{2x}^{\mathrm{3}} +\mathrm{2x}+\mathrm{3} \\ $$$$\mathrm{then}\:\lambda\:=\:\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\:\left(\mathrm{2x}^{\mathrm{3}} +\mathrm{2x}+\mathrm{3}\right)\mathrm{dx}\:=\:\left[\:\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\:+\:\mathrm{x}^{\mathrm{2}} +\mathrm{3x}\:\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$\:\underline{=\:\mathrm{128}+\mathrm{16}+\mathrm{12}\:=\:\mathrm{156}\:}\: \\ $$$$ \\ $$
