Question Number 669 by 112358 last updated on 21/Feb/15
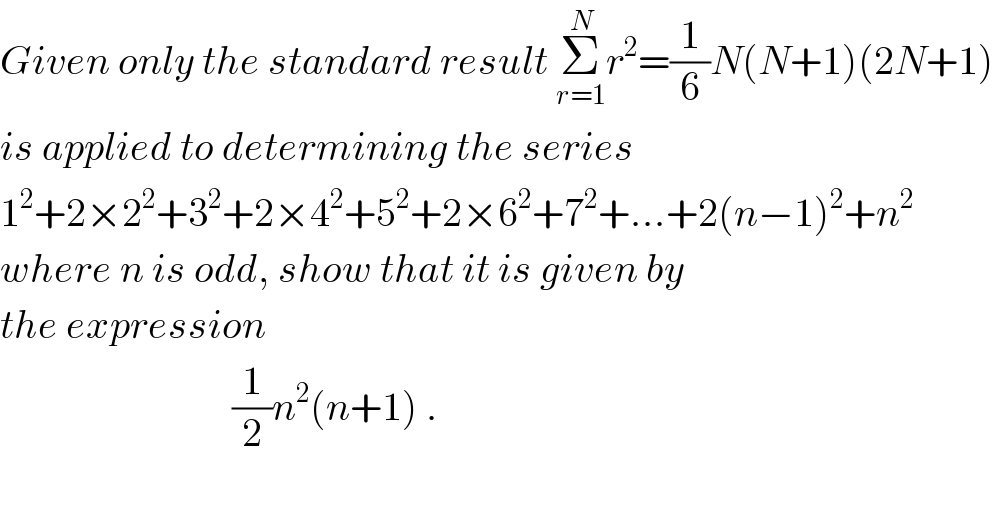
$${Given}\:{only}\:{the}\:{standard}\:{result}\:\underset{{r}=\mathrm{1}} {\overset{{N}} {\sum}}{r}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}{N}\left({N}+\mathrm{1}\right)\left(\mathrm{2}{N}+\mathrm{1}\right)\: \\ $$$${is}\:{applied}\:{to}\:{determining}\:{the}\:{series} \\ $$$$\mathrm{1}^{\mathrm{2}} +\mathrm{2}×\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}×\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{2}×\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} +…+\mathrm{2}\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$$${where}\:{n}\:{is}\:{odd},\:{show}\:{that}\:{it}\:{is}\:{given}\:{by} \\ $$$${the}\:{expression} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\:. \\ $$$$ \\ $$
Answered by 123456 last updated on 21/Feb/15
![n is odd n=2k+1⇔k=((n−1)/2) S=1^2 +2×2^2 +3^2 +2×4^2 +∙∙∙+2×(2k)^2 +(2k+1)^2 =[1^2 +3^2 +∙∙∙+(2k+1)^2 ]+2[2^2 +4^2 +∙∙∙+(2k)^2 ] =S_1 +2S_2 S_1 =1^2 +3^2 +∙∙∙+(2k+1)^2 =Σ_(r=0) ^k (2r+1)^2 =Σ_(r=1) ^(k+1) [2(r−1)+1]^2 =Σ_(r=1) ^(k+1) (2r−1)^2 =(1/3)(k+1)(2k+1)(2k+3) S_2 =2^2 +4^2 +∙∙∙+(2k)^2 =Σ_(r=1) ^k (2r)^2 =4Σ_(r=1) ^k r^2 =4×(1/6)k(k+1)(2k+1) =(2/3)k(k+1)(2k+1) S=S_1 +2S_2 =(1/3)(k+1)(2k+1)(2k+3)+(4/3)k(k+1)(2k+1) =(1/3)(k+1)(2k+1)(2k+3+4k) =(1/3)(k+1)(2k+1)(6k+3) =(k+1)(2k+1)^2 =(k+1)n^2 =(((n−1)/2)+1)n^2 =(1/2)n^2 (n+1)](https://www.tinkutara.com/question/Q670.png)
$${n}\:{is}\:{odd} \\ $$$${n}=\mathrm{2}{k}+\mathrm{1}\Leftrightarrow{k}=\frac{{n}−\mathrm{1}}{\mathrm{2}} \\ $$$${S}=\mathrm{1}^{\mathrm{2}} +\mathrm{2}×\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}×\mathrm{4}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{2}×\left(\mathrm{2}{k}\right)^{\mathrm{2}} +\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\left[\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \right]+\mathrm{2}\left[\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\left(\mathrm{2}{k}\right)^{\mathrm{2}} \right] \\ $$$$={S}_{\mathrm{1}} +\mathrm{2}{S}_{\mathrm{2}} \\ $$$${S}_{\mathrm{1}} =\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} =\underset{{r}=\mathrm{0}} {\overset{{k}} {\sum}}\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\underset{{r}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\sum}}\left[\mathrm{2}\left({r}−\mathrm{1}\right)+\mathrm{1}\right]^{\mathrm{2}} =\underset{{r}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\sum}}\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right) \\ $$$${S}_{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\left(\mathrm{2}{k}\right)^{\mathrm{2}} =\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\mathrm{2}{r}\right)^{\mathrm{2}} \\ $$$$=\mathrm{4}\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}{r}^{\mathrm{2}} =\mathrm{4}×\frac{\mathrm{1}}{\mathrm{6}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$${S}={S}_{\mathrm{1}} +\mathrm{2}{S}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)+\frac{\mathrm{4}}{\mathrm{3}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}+\mathrm{4}{k}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{6}{k}+\mathrm{3}\right) \\ $$$$=\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\left({k}+\mathrm{1}\right){n}^{\mathrm{2}} \\ $$$$=\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right){n}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right) \\ $$
Commented by 123456 last updated on 21/Feb/15
![S_1 =Σ_(r=0) ^k (2r+1)^2 =Σ_(r=0) ^k 4r^2 +4r+1=1+Σ_(r=1) ^k 4r^2 −4r+1 S_1 =Σ_(r=1) ^(k+1) (2r−1)^2 =Σ_(r=1) ^(k+1) 4r^2 −4r+1=(2k+1)^2 +Σ_(r=1) ^k 4r^2 −4r+1 2S_1 =1+(2k+1)^2 +Σ_(r=1) ^k 8r^2 +2 2S_1 =1+4k^2 +4k+1+8Σ_(r=1) ^k r^2 +2Σ_(r=1) ^k 1 =4k^2 +4k+2+8×(1/6)k(k+1)(2k+1)+2k =4k(k+1)+2+(4/3)k(k+1)(2k+1)+2k S_1 =2k(k+1)+(2/3)k(k+1)(2k+1)+(k+1) =2k(k+1)(1+((2k+1)/3))+(k+1) =2k(k+1)((2k+4)/3)+(k+1) =(k+1)[((4k(k+2))/3)+1] =(k+1)((4k^2 +8k+3)/3) =(1/3)(k+1)(2k+1)(2k+3)](https://www.tinkutara.com/question/Q671.png)
$${S}_{\mathrm{1}} =\underset{{r}=\mathrm{0}} {\overset{{k}} {\sum}}\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} =\underset{{r}=\mathrm{0}} {\overset{{k}} {\sum}}\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+\mathrm{1}=\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{1} \\ $$$${S}_{\mathrm{1}} =\underset{{r}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\sum}}\left(\mathrm{2}{r}−\mathrm{1}\right)^{\mathrm{2}} =\underset{{r}=\mathrm{1}} {\overset{{k}+\mathrm{1}} {\sum}}\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{1}=\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} +\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{1} \\ $$$$\mathrm{2}{S}_{\mathrm{1}} =\mathrm{1}+\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} +\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}\mathrm{8}{r}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{2}{S}_{\mathrm{1}} =\mathrm{1}+\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{1}+\mathrm{8}\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}{r}^{\mathrm{2}} +\mathrm{2}\underset{{r}=\mathrm{1}} {\overset{{k}} {\sum}}\mathrm{1} \\ $$$$=\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{2}+\mathrm{8}×\frac{\mathrm{1}}{\mathrm{6}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)+\mathrm{2}{k} \\ $$$$=\mathrm{4}{k}\left({k}+\mathrm{1}\right)+\mathrm{2}+\frac{\mathrm{4}}{\mathrm{3}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)+\mathrm{2}{k} \\ $$$${S}_{\mathrm{1}} =\mathrm{2}{k}\left({k}+\mathrm{1}\right)+\frac{\mathrm{2}}{\mathrm{3}}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)+\left({k}+\mathrm{1}\right) \\ $$$$=\mathrm{2}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{1}+\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{3}}\right)+\left({k}+\mathrm{1}\right) \\ $$$$=\mathrm{2}{k}\left({k}+\mathrm{1}\right)\frac{\mathrm{2}{k}+\mathrm{4}}{\mathrm{3}}+\left({k}+\mathrm{1}\right) \\ $$$$=\left({k}+\mathrm{1}\right)\left[\frac{\mathrm{4}{k}\left({k}+\mathrm{2}\right)}{\mathrm{3}}+\mathrm{1}\right] \\ $$$$=\left({k}+\mathrm{1}\right)\frac{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{3}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right) \\ $$
Commented by 112358 last updated on 21/Feb/15

$${Thanks} \\ $$
