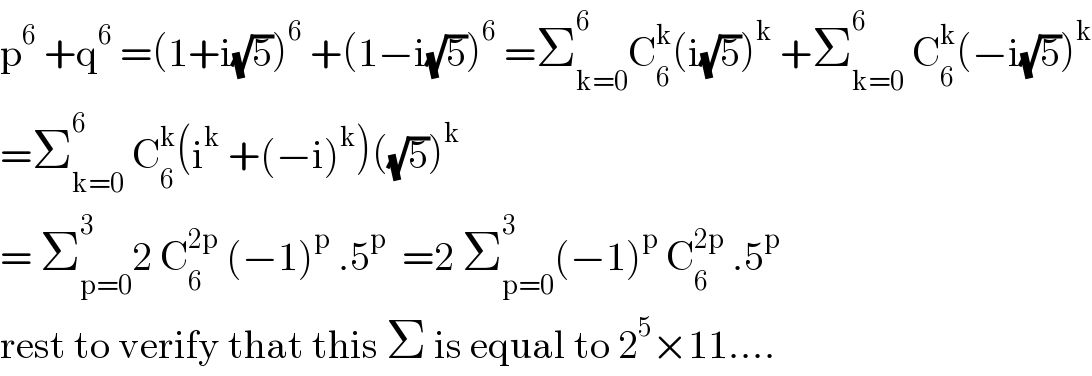Menu Close

Given-p-1-i-5-and-q-1-i-5-prove-that-p-6-q-6-2-5-11-

Tinku Tara 0 Comments
Pin




Question Number 138014 by bobhans last updated on 09/Apr/21
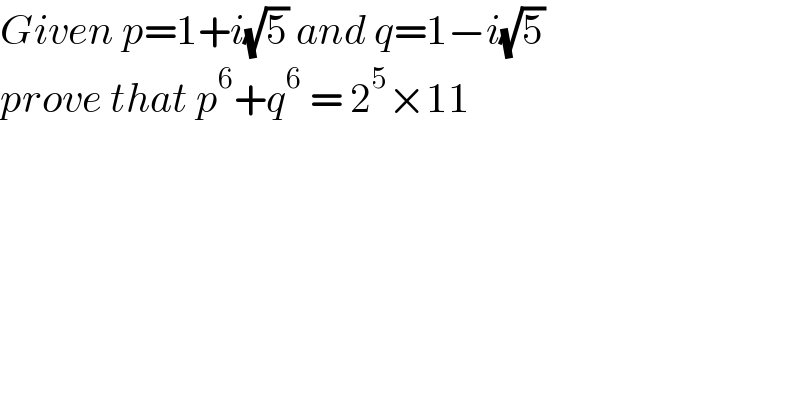
Given p=1+i(√5) and q=1−i(√5) prove that p^6 +q^6 = 2^5 ×11
$${Given}\:{p}=\mathrm{1}+{i}\sqrt{\mathrm{5}}\:{and}\:{q}=\mathrm{1}−{i}\sqrt{\mathrm{5}}\: \\ $$$${prove}\:{that}\:{p}^{\mathrm{6}} +{q}^{\mathrm{6}} \:=\:\mathrm{2}^{\mathrm{5}} ×\mathrm{11} \\ $$
Answered by bobhans last updated on 09/Apr/21
from the given we have ⇒x^2 −2x+6 = 0 has the roots { ((x_1 = p=1+i(√5))),((x_2 = q =1−i(√5))) :} ⇒by Vieta′s rule { ((p+q=2)),((pq = 6)) :} we want to find p^6 +q^6 . (p^3 )^2 +(q^3 )^2 = [ p^3 +q^3 ]^2 −2(pq)^3 = [ (p+q)^3 −3pq(p+q)]^2 −2(pq)^3 = [ 8−3(6)(2)]^2 −2(6)^3 = [ −28 ]^2 −2(216) =784−432 = 352 = 2^5 ×11
$$\:{from}\:{the}\:{given}\:{we}\:{have}\: \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{6}\:=\:\mathrm{0}\:{has}\:{the}\:{roots} \\ $$$$\:\begin{cases}{{x}_{\mathrm{1}} =\:{p}=\mathrm{1}+{i}\sqrt{\mathrm{5}}}\\{{x}_{\mathrm{2}} =\:{q}\:=\mathrm{1}−{i}\sqrt{\mathrm{5}}}\end{cases} \\ $$$$\Rightarrow{by}\:{Vieta}'{s}\:{rule}\:\begin{cases}{{p}+{q}=\mathrm{2}}\\{{pq}\:=\:\mathrm{6}}\end{cases} \\ $$$${we}\:{want}\:{to}\:{find}\:{p}^{\mathrm{6}} +{q}^{\mathrm{6}} . \\ $$$$\left({p}^{\mathrm{3}} \right)^{\mathrm{2}} +\left({q}^{\mathrm{3}} \right)^{\mathrm{2}} \:=\:\left[\:{p}^{\mathrm{3}} +{q}^{\mathrm{3}} \:\right]^{\mathrm{2}} −\mathrm{2}\left({pq}\right)^{\mathrm{3}} \\ $$$$\:=\:\left[\:\left({p}+{q}\right)^{\mathrm{3}} −\mathrm{3}{pq}\left({p}+{q}\right)\right]^{\mathrm{2}} −\mathrm{2}\left({pq}\right)^{\mathrm{3}} \\ $$$$=\:\left[\:\mathrm{8}−\mathrm{3}\left(\mathrm{6}\right)\left(\mathrm{2}\right)\right]^{\mathrm{2}} −\mathrm{2}\left(\mathrm{6}\right)^{\mathrm{3}} \\ $$$$=\:\left[\:−\mathrm{28}\:\right]^{\mathrm{2}} −\mathrm{2}\left(\mathrm{216}\right) \\ $$$$=\mathrm{784}−\mathrm{432}\:=\:\mathrm{352}\:=\:\mathrm{2}^{\mathrm{5}} ×\mathrm{11} \\ $$
Commented by bobhans last updated on 09/Apr/21
request mr Liki
$${request}\:{mr}\:{Liki} \\ $$
Commented by SLVR last updated on 09/Apr/21
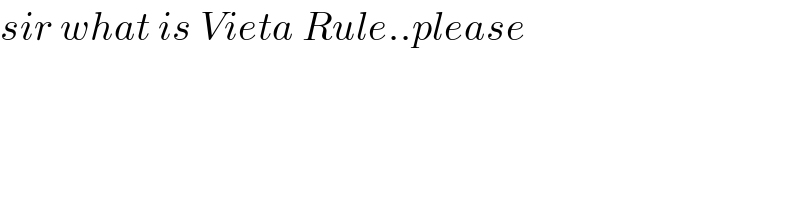
sir what is Vieta Rule..please
$${sir}\:{what}\:{is}\:{Vieta}\:{Rule}..{please} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Apr/21
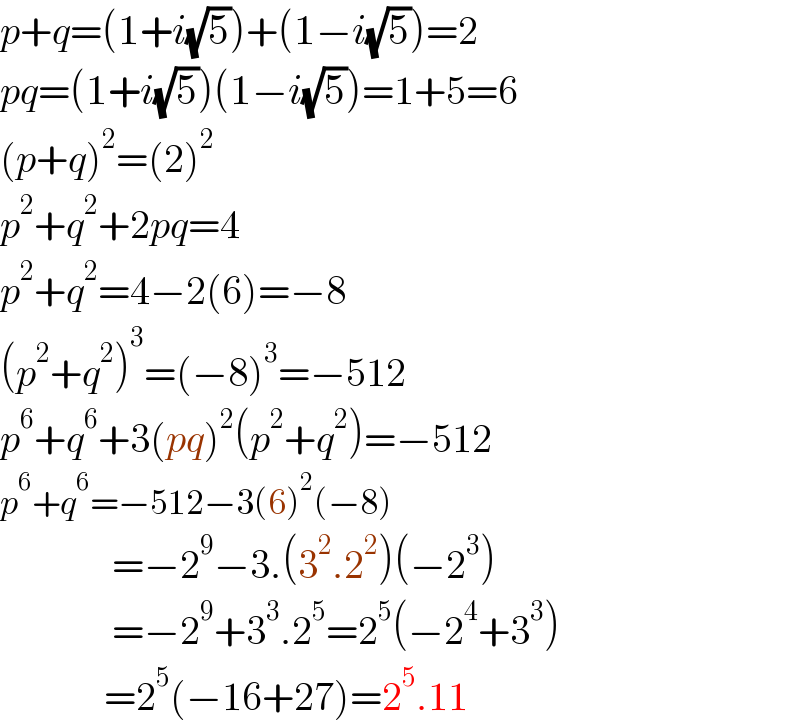
p+q=(1+i(√5))+(1−i(√5))=2 pq=(1+i(√5))(1−i(√5))=1+5=6 (p+q)^2 =(2)^2 p^2 +q^2 +2pq=4 p^2 +q^2 =4−2(6)=−8 (p^2 +q^2 )^3 =(−8)^3 =−512 p^6 +q^6 +3(pq)^2 (p^2 +q^2 )=−512 p^6 +q^6 =−512−3(6)^2 (−8) =−2^9 −3.(3^2 .2^2 )(−2^3 ) =−2^9 +3^3 .2^5 =2^5 (−2^4 +3^3 ) =2^5 (−16+27)=2^5 .11
$${p}+{q}=\left(\mathrm{1}+{i}\sqrt{\mathrm{5}}\right)+\left(\mathrm{1}−{i}\sqrt{\mathrm{5}}\right)=\mathrm{2} \\ $$$${pq}=\left(\mathrm{1}+{i}\sqrt{\mathrm{5}}\right)\left(\mathrm{1}−{i}\sqrt{\mathrm{5}}\right)=\mathrm{1}+\mathrm{5}=\mathrm{6} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} =\left(\mathrm{2}\right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{2}{pq}=\mathrm{4} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{4}−\mathrm{2}\left(\mathrm{6}\right)=−\mathrm{8} \\ $$$$\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)^{\mathrm{3}} =\left(−\mathrm{8}\right)^{\mathrm{3}} =−\mathrm{512} \\ $$$${p}^{\mathrm{6}} +{q}^{\mathrm{6}} +\mathrm{3}\left({pq}\right)^{\mathrm{2}} \left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=−\mathrm{512} \\ $$$${p}^{\mathrm{6}} +{q}^{\mathrm{6}} =−\mathrm{512}−\mathrm{3}\left(\mathrm{6}\right)^{\mathrm{2}} \left(−\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{2}^{\mathrm{9}} −\mathrm{3}.\left(\mathrm{3}^{\mathrm{2}} .\mathrm{2}^{\mathrm{2}} \right)\left(−\mathrm{2}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{2}^{\mathrm{9}} +\mathrm{3}^{\mathrm{3}} .\mathrm{2}^{\mathrm{5}} =\mathrm{2}^{\mathrm{5}} \left(−\mathrm{2}^{\mathrm{4}} +\mathrm{3}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{5}} \left(−\mathrm{16}+\mathrm{27}\right)=\mathrm{2}^{\mathrm{5}} .\mathrm{11} \\ $$
Answered by mathmax by abdo last updated on 10/Apr/21
p^6 +q^6 =(1+i(√5))^6 +(1−i(√5))^6 =Σ_(k=0) ^6 C_6 ^k (i(√5))^k +Σ_(k=0) ^6 C_6 ^k (−i(√5))^k =Σ_(k=0) ^6 C_6 ^k (i^k +(−i)^k )((√5))^k = Σ_(p=0) ^3 2 C_6 ^(2p) (−1)^p .5^p =2 Σ_(p=0) ^3 (−1)^p C_6 ^(2p) .5^p rest to verify that this Σ is equal to 2^5 ×11....
$$\mathrm{p}^{\mathrm{6}} \:+\mathrm{q}^{\mathrm{6}} \:=\left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{5}}\right)^{\mathrm{6}} \:+\left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{5}}\right)^{\mathrm{6}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \left(\mathrm{i}\sqrt{\mathrm{5}}\right)^{\mathrm{k}} \:+\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \left(−\mathrm{i}\sqrt{\mathrm{5}}\right)^{\mathrm{k}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \left(\mathrm{i}^{\mathrm{k}} \:+\left(−\mathrm{i}\right)^{\mathrm{k}} \right)\left(\sqrt{\mathrm{5}}\right)^{\mathrm{k}} \\ $$$$=\:\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{3}} \mathrm{2}\:\mathrm{C}_{\mathrm{6}} ^{\mathrm{2p}} \:\left(−\mathrm{1}\right)^{\mathrm{p}} \:.\mathrm{5}^{\mathrm{p}} \:\:=\mathrm{2}\:\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{3}} \left(−\mathrm{1}\right)^{\mathrm{p}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{2p}} \:.\mathrm{5}^{\mathrm{p}} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{verify}\:\mathrm{that}\:\mathrm{this}\:\Sigma\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2}^{\mathrm{5}} ×\mathrm{11}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *