Question Number 142968 by bramlexs22 last updated on 08/Jun/21
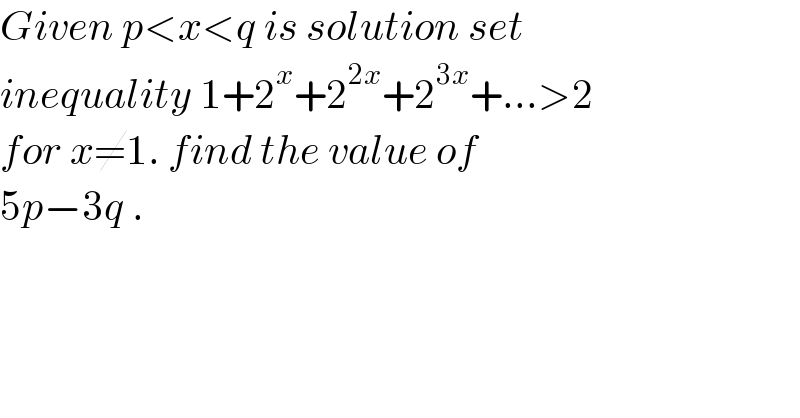
$${Given}\:{p}<{x}<{q}\:{is}\:{solution}\:{set} \\ $$$${inequality}\:\mathrm{1}+\mathrm{2}^{{x}} +\mathrm{2}^{\mathrm{2}{x}} +\mathrm{2}^{\mathrm{3}{x}} +…>\mathrm{2} \\ $$$${for}\:{x}\neq\mathrm{1}.\:{find}\:{the}\:{value}\:{of}\: \\ $$$$\mathrm{5}{p}−\mathrm{3}{q}\:. \\ $$
Answered by mr W last updated on 08/Jun/21
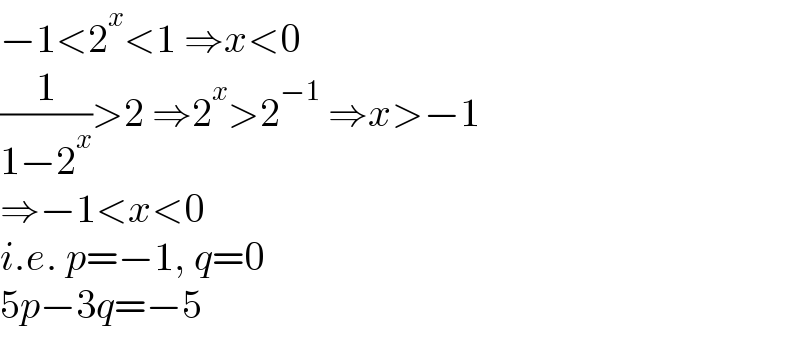
$$−\mathrm{1}<\mathrm{2}^{{x}} <\mathrm{1}\:\Rightarrow{x}<\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}^{{x}} }>\mathrm{2}\:\Rightarrow\mathrm{2}^{{x}} >\mathrm{2}^{−\mathrm{1}} \:\Rightarrow{x}>−\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}<{x}<\mathrm{0} \\ $$$${i}.{e}.\:{p}=−\mathrm{1},\:{q}=\mathrm{0} \\ $$$$\mathrm{5}{p}−\mathrm{3}{q}=−\mathrm{5} \\ $$
