Question Number 134581 by EDWIN88 last updated on 05/Mar/21

$$\mathrm{Given}\:\begin{cases}{\mathrm{sin}\:\mathrm{A}+\mathrm{sin}\:\mathrm{B}=\mathrm{0}.\mathrm{7}}\\{\mathrm{cos}\:\mathrm{A}+\mathrm{cos}\:\mathrm{B}=\mathrm{0}.\mathrm{8}}\end{cases} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}. \\ $$
Answered by liberty last updated on 05/Mar/21
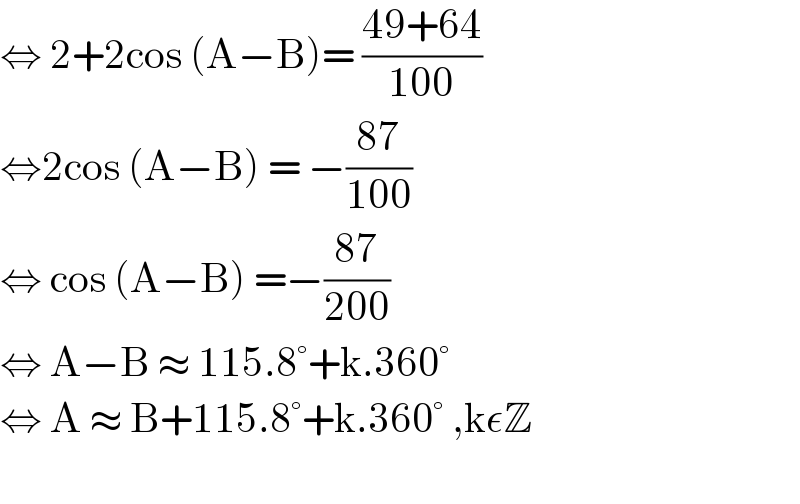
$$\Leftrightarrow\:\mathrm{2}+\mathrm{2cos}\:\left(\mathrm{A}−\mathrm{B}\right)=\:\frac{\mathrm{49}+\mathrm{64}}{\mathrm{100}} \\ $$$$\Leftrightarrow\mathrm{2cos}\:\left(\mathrm{A}−\mathrm{B}\right)\:=\:−\frac{\mathrm{87}}{\mathrm{100}} \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\left(\mathrm{A}−\mathrm{B}\right)\:=−\frac{\mathrm{87}}{\mathrm{200}} \\ $$$$\Leftrightarrow\:\mathrm{A}−\mathrm{B}\:\approx\:\mathrm{115}.\mathrm{8}°+\mathrm{k}.\mathrm{360}° \\ $$$$\Leftrightarrow\:\mathrm{A}\:\approx\:\mathrm{B}+\mathrm{115}.\mathrm{8}°+\mathrm{k}.\mathrm{360}°\:,\mathrm{k}\epsilon\mathbb{Z} \\ $$$$ \\ $$
Answered by mr W last updated on 05/Mar/21
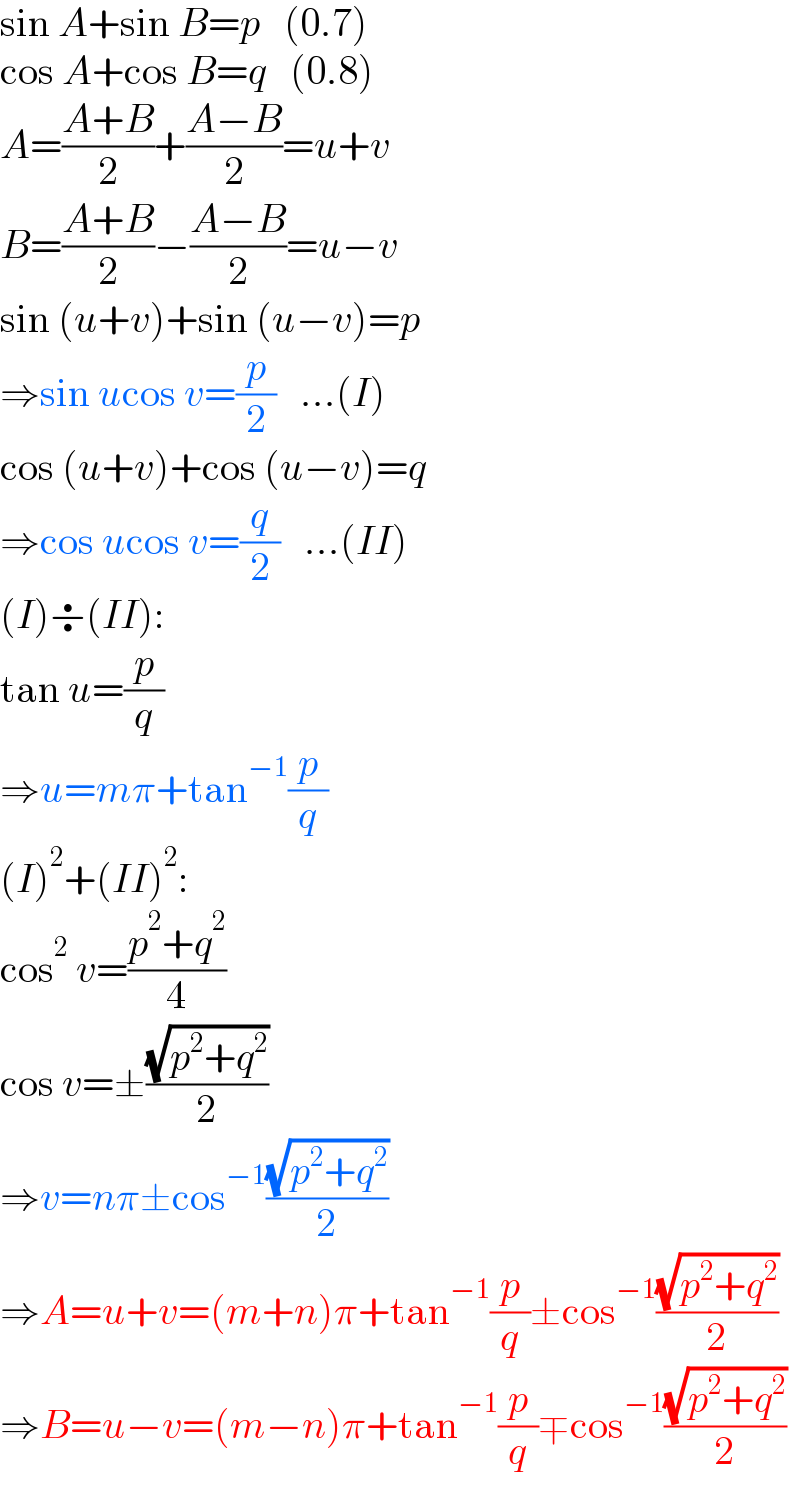
$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}={p}\:\:\:\left(\mathrm{0}.\mathrm{7}\right) \\ $$$$\mathrm{cos}\:{A}+\mathrm{cos}\:{B}={q}\:\:\:\left(\mathrm{0}.\mathrm{8}\right) \\ $$$${A}=\frac{{A}+{B}}{\mathrm{2}}+\frac{{A}−{B}}{\mathrm{2}}={u}+{v} \\ $$$${B}=\frac{{A}+{B}}{\mathrm{2}}−\frac{{A}−{B}}{\mathrm{2}}={u}−{v} \\ $$$$\mathrm{sin}\:\left({u}+{v}\right)+\mathrm{sin}\:\left({u}−{v}\right)={p} \\ $$$$\Rightarrow\mathrm{sin}\:{u}\mathrm{cos}\:{v}=\frac{{p}}{\mathrm{2}}\:\:\:…\left({I}\right) \\ $$$$\mathrm{cos}\:\left({u}+{v}\right)+\mathrm{cos}\:\left({u}−{v}\right)={q} \\ $$$$\Rightarrow\mathrm{cos}\:{u}\mathrm{cos}\:{v}=\frac{{q}}{\mathrm{2}}\:\:\:…\left({II}\right) \\ $$$$\left({I}\right)\boldsymbol{\div}\left({II}\right): \\ $$$$\mathrm{tan}\:{u}=\frac{{p}}{{q}} \\ $$$$\Rightarrow{u}={m}\pi+\mathrm{tan}^{−\mathrm{1}} \frac{{p}}{{q}} \\ $$$$\left({I}\right)^{\mathrm{2}} +\left({II}\right)^{\mathrm{2}} : \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{v}=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{cos}\:{v}=\pm\frac{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{v}={n}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{A}={u}+{v}=\left({m}+{n}\right)\pi+\mathrm{tan}^{−\mathrm{1}} \frac{{p}}{{q}}\pm\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{B}={u}−{v}=\left({m}−{n}\right)\pi+\mathrm{tan}^{−\mathrm{1}} \frac{{p}}{{q}}\mp\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 05/Mar/21

$$\Rightarrow\mathrm{2sin}\:\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}\right)=\frac{\mathrm{7}}{\mathrm{10}} \\ $$$$\Rightarrow\mathrm{2cos}\:\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}\right)=\frac{\mathrm{8}}{\mathrm{10}} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{tan}\:\left(\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}\right)=\:\frac{\mathrm{7}}{\mathrm{8}};\:\mathrm{A}+\mathrm{B}=\mathrm{82}.\mathrm{24}°+\mathrm{2k}\pi \\ $$$$\left(\mathrm{ii}\right)\mathrm{2}+\mathrm{2cos}\:\left(\mathrm{A}−\mathrm{B}\right)=\:\frac{\mathrm{113}}{\mathrm{100}} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\mathrm{A}−\mathrm{B}\right)=\:−\frac{\mathrm{87}}{\mathrm{200}}\:;\:\mathrm{A}−\mathrm{B}\:=\:\mathrm{115}.\mathrm{78}°+\mathrm{2k}\pi \\ $$$$\mathrm{Thus}\:\begin{cases}{\mathrm{A}=\mathrm{99}.\mathrm{01}°+\mathrm{2k}\pi}\\{\mathrm{B}=−\mathrm{16}.\mathrm{77}°+\mathrm{2k}\pi}\end{cases} \\ $$$$ \\ $$
