Question Number 136749 by EDWIN88 last updated on 25/Mar/21
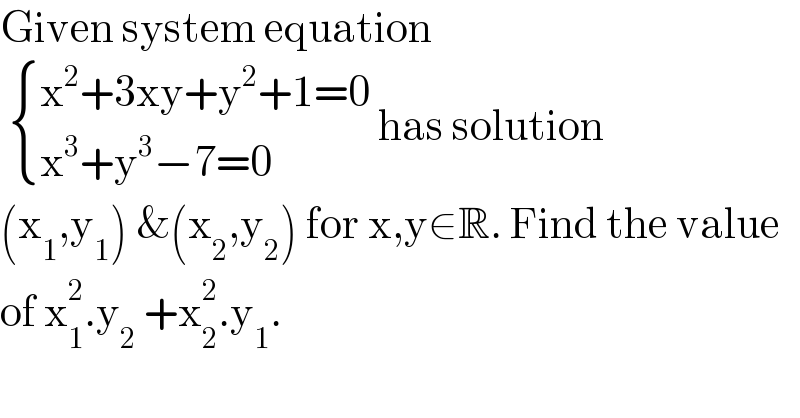
$$\mathrm{Given}\:\mathrm{system}\:\mathrm{equation}\: \\ $$$$\:\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{3xy}+\mathrm{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}}\\{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} −\mathrm{7}=\mathrm{0}}\end{cases}\:\mathrm{has}\:\mathrm{solution}\: \\ $$$$\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} \right)\:\&\left(\mathrm{x}_{\mathrm{2}} ,\mathrm{y}_{\mathrm{2}} \right)\:\mathrm{for}\:\mathrm{x},\mathrm{y}\in\mathbb{R}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} .\mathrm{y}_{\mathrm{2}} \:+\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} .\mathrm{y}_{\mathrm{1}} .\: \\ $$
Answered by MJS_new last updated on 25/Mar/21
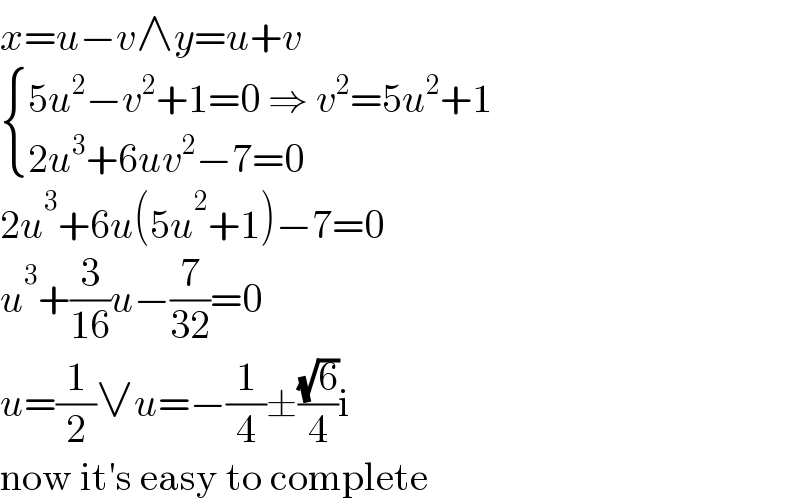
$${x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\begin{cases}{\mathrm{5}{u}^{\mathrm{2}} −{v}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\:{v}^{\mathrm{2}} =\mathrm{5}{u}^{\mathrm{2}} +\mathrm{1}}\\{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}{uv}^{\mathrm{2}} −\mathrm{7}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}{u}\left(\mathrm{5}{u}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{7}=\mathrm{0} \\ $$$${u}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{16}}{u}−\frac{\mathrm{7}}{\mathrm{32}}=\mathrm{0} \\ $$$${u}=\frac{\mathrm{1}}{\mathrm{2}}\vee{u}=−\frac{\mathrm{1}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{4}}\mathrm{i} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{complete} \\ $$
Answered by bramlexs22 last updated on 26/Mar/21
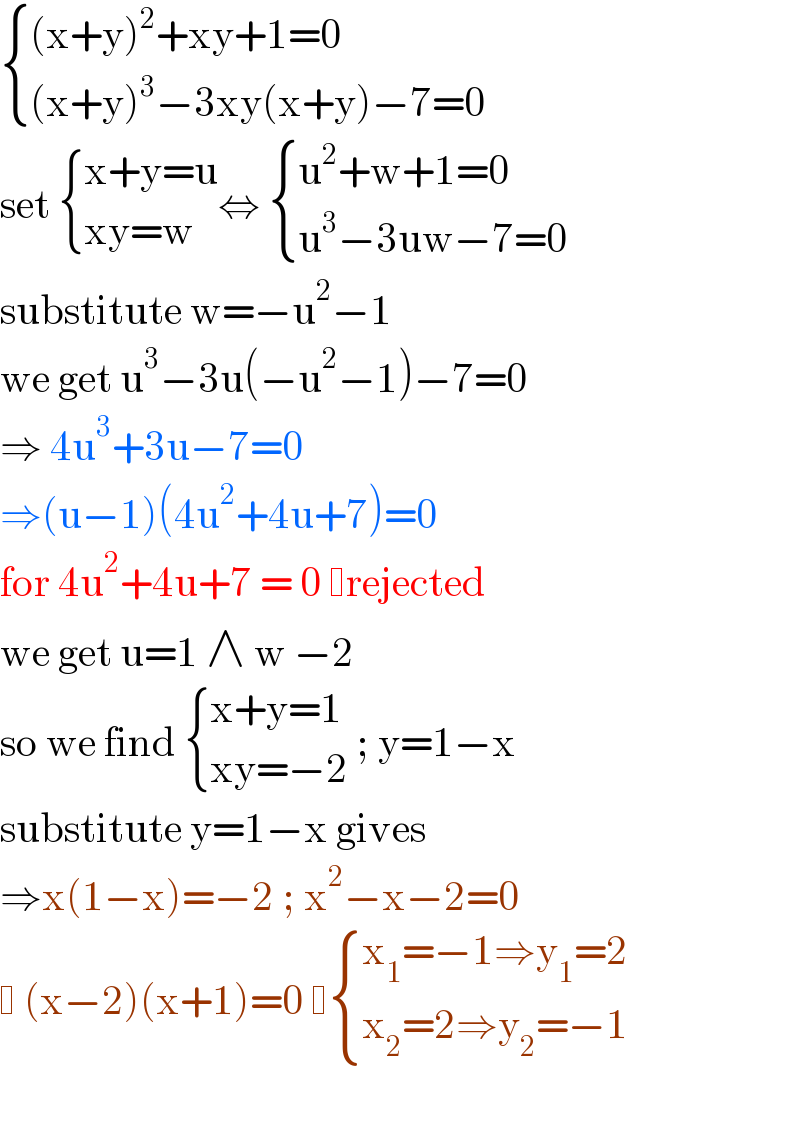
$$\begin{cases}{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} +\mathrm{xy}+\mathrm{1}=\mathrm{0}}\\{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} −\mathrm{3xy}\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{7}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{set}\:\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{u}}\\{\mathrm{xy}=\mathrm{w}}\end{cases}\Leftrightarrow\:\begin{cases}{\mathrm{u}^{\mathrm{2}} +\mathrm{w}+\mathrm{1}=\mathrm{0}}\\{\mathrm{u}^{\mathrm{3}} −\mathrm{3uw}−\mathrm{7}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{substitute}\:\mathrm{w}=−\mathrm{u}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{u}^{\mathrm{3}} −\mathrm{3u}\left(−\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{7}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4u}^{\mathrm{3}} +\mathrm{3u}−\mathrm{7}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{4u}^{\mathrm{2}} +\mathrm{4u}+\mathrm{7}\right)=\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{4u}^{\mathrm{2}} +\mathrm{4u}+\mathrm{7}\:=\:\mathrm{0}\: \mathrm{rejected}\: \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{u}=\mathrm{1}\:\wedge\:\mathrm{w}\:−\mathrm{2} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{find}\:\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{1}}\\{\mathrm{xy}=−\mathrm{2}}\end{cases}\:;\:\mathrm{y}=\mathrm{1}−\mathrm{x} \\ $$$$\mathrm{substitute}\:\mathrm{y}=\mathrm{1}−\mathrm{x}\:\mathrm{gives} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)=−\mathrm{2}\:;\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$ \:\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0}\: \begin{cases}{\mathrm{x}_{\mathrm{1}} =−\mathrm{1}\Rightarrow\mathrm{y}_{\mathrm{1}} =\mathrm{2}}\\{\mathrm{x}_{\mathrm{2}} =\mathrm{2}\Rightarrow\mathrm{y}_{\mathrm{2}} =−\mathrm{1}}\end{cases} \\ $$$$ \\ $$
