Menu Close

given-that-and-are-roots-of-the-equation-x-2-5x-4-0-gt-0-and-gt-0-find-an-equation-whose-roots-are-and-how-do-i-find-

Tinku Tara 0 Comments
Pin




Question Number 70617 by Rio Michael last updated on 06/Oct/19
given that α and β are roots of the equation x^2 −5x + 4 =0 α>0 and β >0 find an equation whose roots are (√α) and (√β) how do i find (√(α )) + (√β)
$${given}\:{that}\:\:\alpha\:{and}\:\beta\:{are}\:{roots}\:{of}\:{the}\:{equation}\:{x}^{\mathrm{2}} −\mathrm{5}{x}\:+\:\mathrm{4}\:=\mathrm{0}\: \\ $$$$\alpha>\mathrm{0}\:{and}\:\beta\:>\mathrm{0} \\ $$$${find}\:{an}\:{equation}\:{whose}\:{roots}\:{are}\:\sqrt{\alpha}\:{and}\:\sqrt{\beta}\: \\ $$$$ \\ $$$${how}\:{do}\:{i}\:{find}\:\:\sqrt{\alpha\:}\:+\:\sqrt{\beta}\: \\ $$
Answered by mr W last updated on 06/Oct/19
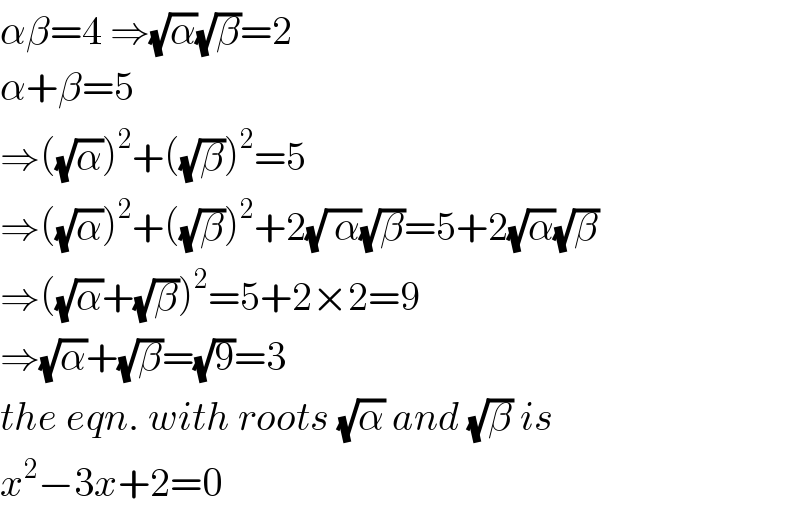
αβ=4 ⇒(√α)(√β)=2 α+β=5 ⇒((√α))^2 +((√β))^2 =5 ⇒((√α))^2 +((√β))^2 +2(√( α))(√β)=5+2(√α)(√β) ⇒((√α)+(√β))^2 =5+2×2=9 ⇒(√α)+(√β)=(√9)=3 the eqn. with roots (√α) and (√β) is x^2 −3x+2=0
$$\alpha\beta=\mathrm{4}\:\Rightarrow\sqrt{\alpha}\sqrt{\beta}=\mathrm{2} \\ $$$$\alpha+\beta=\mathrm{5}\: \\ $$$$\Rightarrow\left(\sqrt{\alpha}\right)^{\mathrm{2}} +\left(\sqrt{\beta}\right)^{\mathrm{2}} =\mathrm{5} \\ $$$$\Rightarrow\left(\sqrt{\alpha}\right)^{\mathrm{2}} +\left(\sqrt{\beta}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\:\alpha}\sqrt{\beta}=\mathrm{5}+\mathrm{2}\sqrt{\alpha}\sqrt{\beta} \\ $$$$\Rightarrow\left(\sqrt{\alpha}+\sqrt{\beta}\right)^{\mathrm{2}} =\mathrm{5}+\mathrm{2}×\mathrm{2}=\mathrm{9} \\ $$$$\Rightarrow\sqrt{\alpha}+\sqrt{\beta}=\sqrt{\mathrm{9}}=\mathrm{3} \\ $$$${the}\:{eqn}.\:{with}\:{roots}\:\sqrt{\alpha}\:{and}\:\sqrt{\beta}\:{is} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\mathrm{0} \\ $$
Commented by Rio Michael last updated on 06/Oct/19
thank yiu so much mr W
$${thank}\:{yiu}\:{so}\:{much}\:{mr}\:{W} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *