Question Number 8310 by lepan last updated on 07/Oct/16
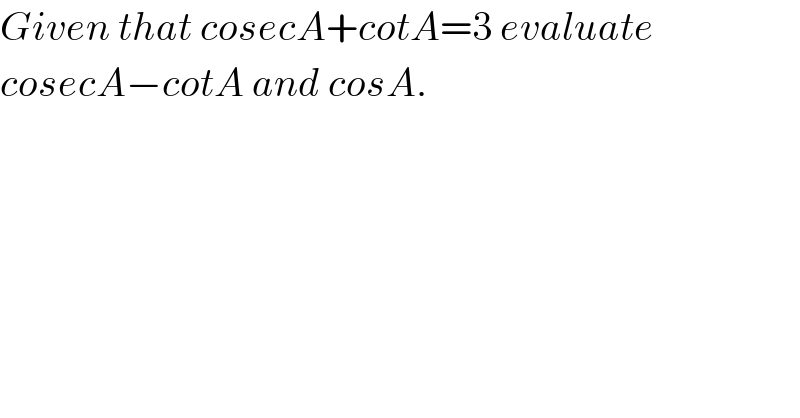
$${Given}\:{that}\:{cosecA}+{cotA}=\mathrm{3}\:{evaluate} \\ $$$${cosecA}−{cotA}\:{and}\:{cosA}. \\ $$$$ \\ $$
Answered by prakash jain last updated on 08/Oct/16
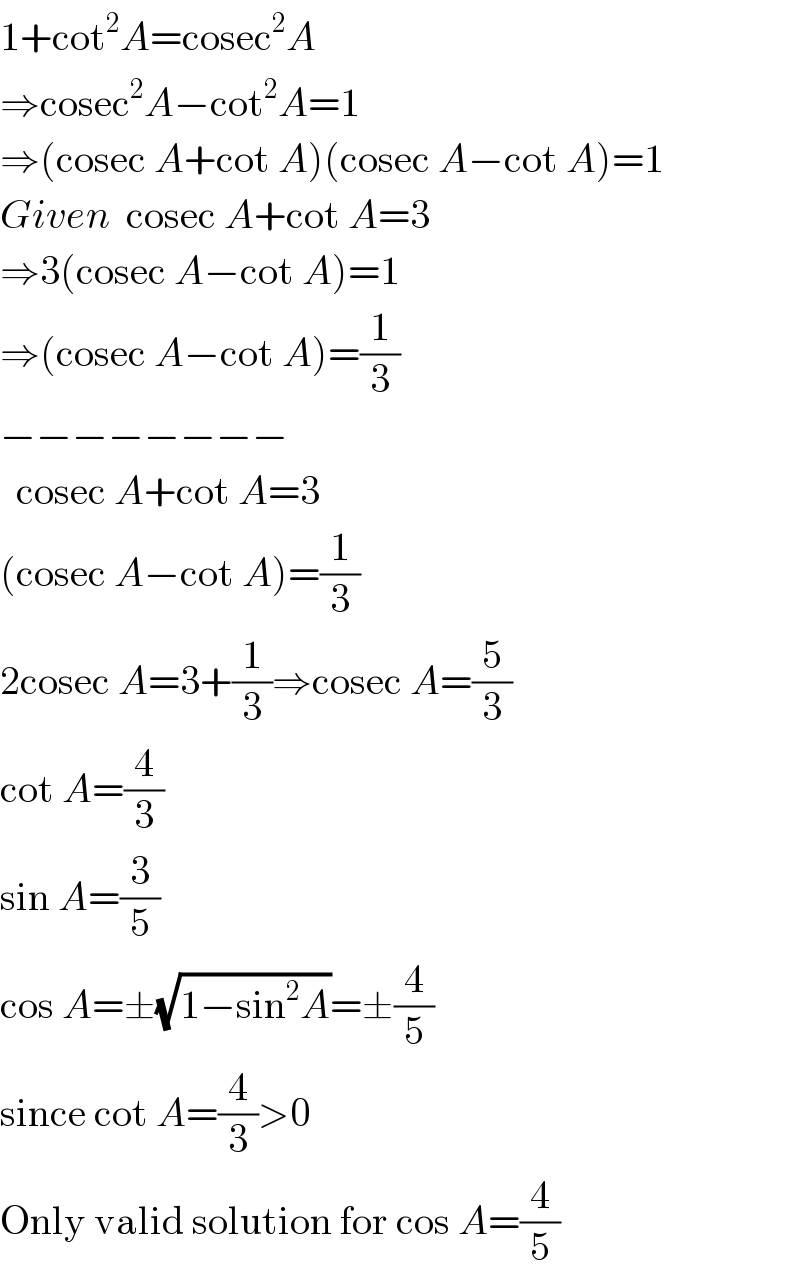
$$\mathrm{1}+\mathrm{cot}^{\mathrm{2}} {A}=\mathrm{cosec}^{\mathrm{2}} {A} \\ $$$$\Rightarrow\mathrm{cosec}^{\mathrm{2}} {A}−\mathrm{cot}^{\mathrm{2}} {A}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{cosec}\:{A}+\mathrm{cot}\:{A}\right)\left(\mathrm{cosec}\:{A}−\mathrm{cot}\:{A}\right)=\mathrm{1} \\ $$$${Given}\:\:\mathrm{cosec}\:{A}+\mathrm{cot}\:{A}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{cosec}\:{A}−\mathrm{cot}\:{A}\right)=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{cosec}\:{A}−\mathrm{cot}\:{A}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$−−−−−−−− \\ $$$$\:\:\mathrm{cosec}\:{A}+\mathrm{cot}\:{A}=\mathrm{3} \\ $$$$\left(\mathrm{cosec}\:{A}−\mathrm{cot}\:{A}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{2cosec}\:{A}=\mathrm{3}+\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow\mathrm{cosec}\:{A}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{cot}\:{A}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{sin}\:{A}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:{A}=\pm\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {A}}=\pm\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{since}\:\mathrm{cot}\:{A}=\frac{\mathrm{4}}{\mathrm{3}}>\mathrm{0} \\ $$$$\mathrm{Only}\:\mathrm{valid}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{cos}\:{A}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$
