Question Number 1139 by 314159 last updated on 30/Jun/15

$${Given}\:{that}\:{f}\:{is}\:{a}\:{polynomial}\:{function}\:{of} \\ $$$${degree}\:\mathrm{8}\:{such}\:{that}\:{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}},{f}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{6}},{f}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${f}\left(\mathrm{4}\right)=\frac{\mathrm{1}}{\mathrm{20}},{f}\left(\mathrm{5}\right)=\frac{\mathrm{1}}{\mathrm{30}},{f}\left(\mathrm{6}\right)=\frac{\mathrm{1}}{\mathrm{42}},{f}\left(\mathrm{7}\right)=\frac{\mathrm{1}}{\mathrm{56}},{f}\left(\mathrm{8}\right)=\frac{\mathrm{1}}{\mathrm{72}} \\ $$$${f}\left(\mathrm{9}\right)=\frac{\mathrm{1}}{\mathrm{90}\:}\:\:.{Find}\:{f}\left(\mathrm{10}\right)\:{and}\:{f}\left(\mathrm{11}\right). \\ $$
Commented by 123456 last updated on 30/Jun/15
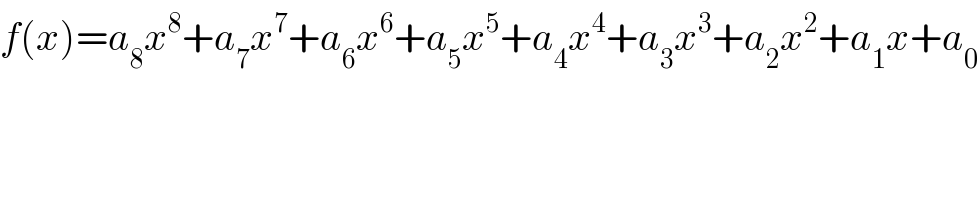
$${f}\left({x}\right)={a}_{\mathrm{8}} {x}^{\mathrm{8}} +{a}_{\mathrm{7}} {x}^{\mathrm{7}} +{a}_{\mathrm{6}} {x}^{\mathrm{6}} +{a}_{\mathrm{5}} {x}^{\mathrm{5}} +{a}_{\mathrm{4}} {x}^{\mathrm{4}} +{a}_{\mathrm{3}} {x}^{\mathrm{3}} +{a}_{\mathrm{2}} {x}^{\mathrm{2}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{0}} \\ $$
Commented by MemoryField last updated on 11/Jul/15
$${sr}\:{bad}\:{english}\:{skill}\:{in}\:{reading} \\ $$$$ \\ $$
