Question Number 142844 by ZiYangLee last updated on 06/Jun/21
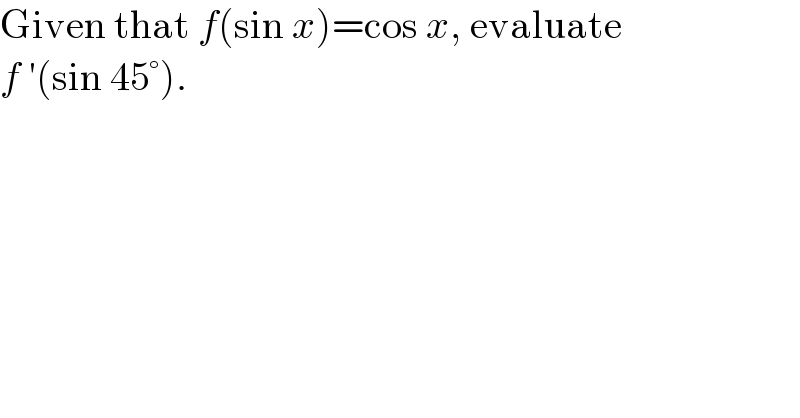
$$\mathrm{Given}\:\mathrm{that}\:{f}\left(\mathrm{sin}\:{x}\right)=\mathrm{cos}\:{x},\:\mathrm{evaluate} \\ $$$${f}\:'\left(\mathrm{sin}\:\mathrm{45}°\right). \\ $$
Answered by meetbhavsar25 last updated on 06/Jun/21
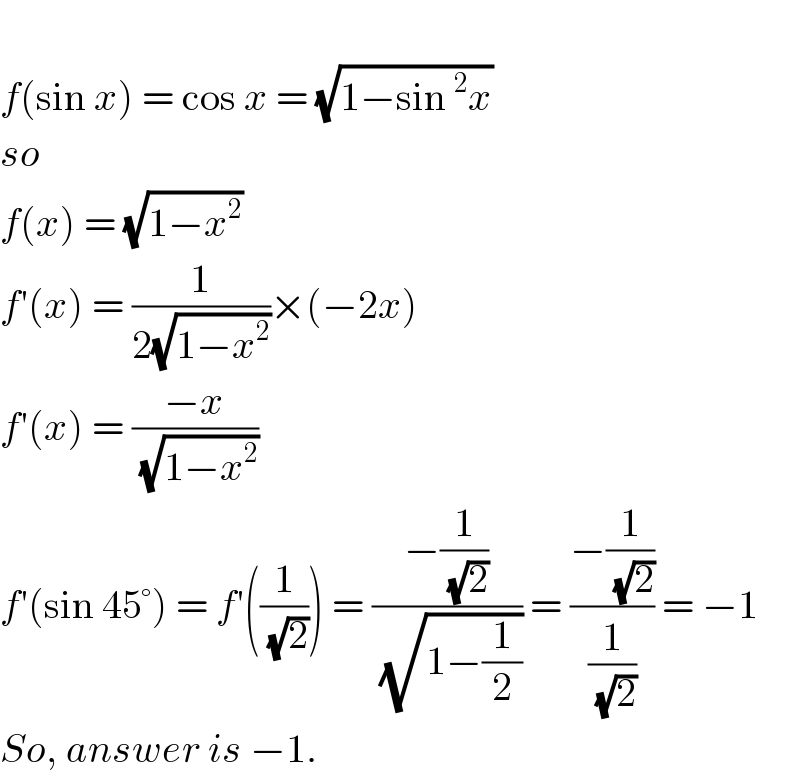
$$ \\ $$$${f}\left(\mathrm{sin}\:{x}\right)\:=\:\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$${so} \\ $$$${f}\left({x}\right)\:=\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}×\left(−\mathrm{2}{x}\right) \\ $$$${f}'\left({x}\right)\:=\:\frac{−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${f}'\left(\mathrm{sin}\:\mathrm{45}°\right)\:=\:{f}'\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:=\:\frac{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}}\:=\:\frac{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\:−\mathrm{1} \\ $$$${So},\:{answer}\:{is}\:−\mathrm{1}. \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jun/21
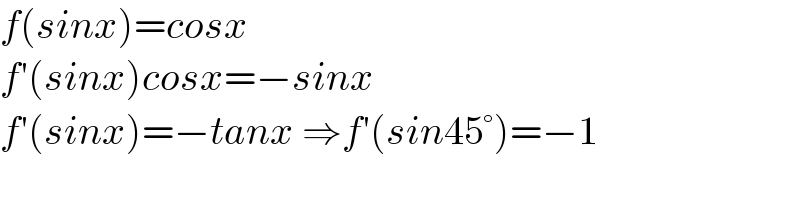
$${f}\left({sinx}\right)={cosx} \\ $$$${f}'\left({sinx}\right){cosx}=−{sinx} \\ $$$${f}'\left({sinx}\right)=−{tanx}\:\Rightarrow{f}'\left({sin}\mathrm{45}°\right)=−\mathrm{1} \\ $$
