Question Number 133179 by abdullahquwatan last updated on 19/Feb/21
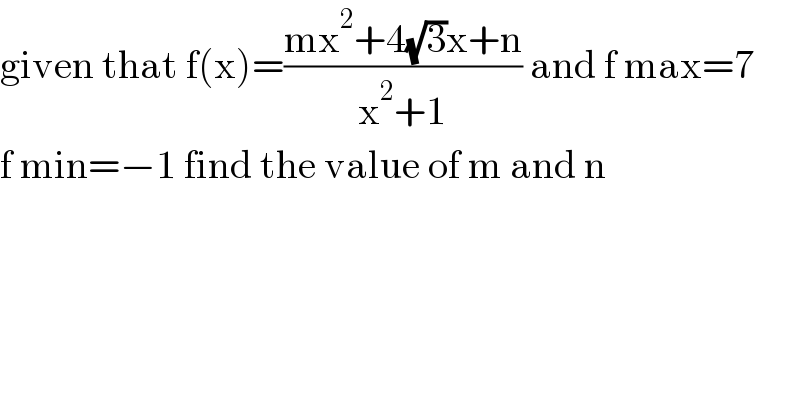
$$\mathrm{given}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{mx}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{n}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{and}\:\mathrm{f}\:\mathrm{max}=\mathrm{7} \\ $$$$\mathrm{f}\:\mathrm{min}=−\mathrm{1}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{m}\:\mathrm{and}\:\mathrm{n} \\ $$
Commented by abdullahquwatan last updated on 20/Feb/21

$$\mathrm{thx} \\ $$
Answered by EDWIN88 last updated on 21/Feb/21

$$\:\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{mx}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{n}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:;\:\mathrm{have} \\ $$$$\mathrm{minimum}\:=\:−\mathrm{1}\:\mathrm{and}\:\mathrm{maximum}\:=\:\mathrm{7}.\:\mathrm{Find} \\ $$$$\mathrm{m}\:\mathrm{and}\:\mathrm{n}.\: \\ $$$$\frac{\mathrm{df}\left(\mathrm{x}\right)}{\mathrm{dx}}\:=\:\frac{\left(\mathrm{2mx}+\mathrm{4}\sqrt{\mathrm{3}}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2x}\left(\mathrm{mx}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{n}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2mx}^{\mathrm{3}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\mathrm{2mx}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{2mx}^{\mathrm{3}} −\mathrm{8}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{2nx}\:=\:\mathrm{0} \\ $$$$−\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2m}−\mathrm{2n}\right)\mathrm{x}+\mathrm{4}\sqrt{\mathrm{3}}\:=\:\mathrm{0}\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\mathrm{have}\:\mathrm{2}\:\mathrm{roots}\:\mathrm{say}\:\mathrm{it}\:\begin{cases}{\mathrm{x}_{\mathrm{1}} \Rightarrow\mathrm{for}\:\mathrm{minimum}\:\mathrm{value}}\\{\mathrm{x}_{\mathrm{2}} \Rightarrow\mathrm{for}\:\mathrm{maximum}\:\mathrm{value}}\end{cases} \\ $$$$\mathrm{consider}\:\mathrm{f}\left(\mathrm{x}_{\mathrm{1}} \right)=\frac{\mathrm{mx}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}_{\mathrm{1}} +\mathrm{n}}{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:\left(\mathrm{m}+\mathrm{1}\right)\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}_{\mathrm{1}} +\left(\mathrm{n}+\mathrm{1}\right)=\mathrm{0}\: \\ $$$$\mathrm{take}\:\mathrm{discriminant}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{12}\:=\:\left(\mathrm{m}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{1}\right)\:;\:\mathrm{mn}+\mathrm{m}+\mathrm{n}=\mathrm{11}…\left(\mathrm{i}\right) \\ $$$$\:\mathrm{consider}\:\mathrm{f}\left(\mathrm{x}_{\mathrm{2}} \right)=\frac{\mathrm{mx}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}_{\mathrm{2}} +\mathrm{n}}{\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{1}}=\:\mathrm{7} \\ $$$$\Rightarrow\left(\mathrm{m}−\mathrm{7}\right)\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}_{\mathrm{2}} +\left(\mathrm{n}−\mathrm{7}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{take}\:\mathrm{discriminant}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{12}\:=\:\left(\mathrm{n}−\mathrm{7}\right)\left(\mathrm{m}−\mathrm{7}\right);\:\mathrm{mn}−\mathrm{7}\left(\mathrm{m}+\mathrm{n}\right)=−\mathrm{37}…\left(\mathrm{ii}\right) \\ $$$$\mathrm{solving}\:\mathrm{for}\:\mathrm{m}\:\&\:\mathrm{n}\: \\ $$$$\left(\mathrm{i}\right)−\left(\mathrm{ii}\right)\Rightarrow\:\mathrm{8}\left(\mathrm{m}+\mathrm{n}\right)=\mathrm{48}\:;\:\mathrm{m}+\mathrm{n}\:=\:\mathrm{6} \\ $$$$\mathrm{substitute}\:\mathrm{to}\:\mathrm{eq}\left(\mathrm{i}\right)\:\rightarrow\mathrm{mn}+\mathrm{6}\:=\:\mathrm{11} \\ $$$$\mathrm{m}\left(\mathrm{6}−\mathrm{m}\right)=\mathrm{5}\:\Rightarrow\mathrm{m}^{\mathrm{2}} −\mathrm{6m}+\mathrm{5}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{m}−\mathrm{1}\right)\left(\mathrm{m}−\mathrm{5}\right)=\mathrm{0}\rightarrow\begin{cases}{\mathrm{m}=\mathrm{1},\mathrm{n}=\mathrm{5}}\\{\mathrm{m}=\mathrm{5},\mathrm{n}=\mathrm{1}}\end{cases} \\ $$$$\mathrm{then}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{5}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{5x}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by bramlexs22 last updated on 21/Feb/21

Commented by bramlexs22 last updated on 21/Feb/21

$$\mathrm{yes}\:\mathrm{correct}\:\mathrm{sir} \\ $$
