Question Number 896 by 112358 last updated on 15/Apr/15
![Given that the velocity v of a body t seconds after passing a point O is found by v^2 =(1/k)[P−(P−kv_o ^2 )e^(−((2kt)/m)) ] determine the distance covered by the body one hour after passing O. The body moves along a straight line. k,P,v_o and m are constants and t is measured in seconds.](https://www.tinkutara.com/question/Q896.png)
$${Given}\:{that}\:{the}\:{velocity}\:{v}\:{of}\:{a}\:{body} \\ $$$${t}\:{seconds}\:{after}\:{passing}\:{a}\:{point}\:{O} \\ $$$${is}\:{found}\:{by} \\ $$$$\:\:\:\:\:\:\:\:{v}^{\mathrm{2}} =\frac{\mathrm{1}}{{k}}\left[{P}−\left({P}−{kv}_{{o}} ^{\mathrm{2}} \right){e}^{−\frac{\mathrm{2}{kt}}{{m}}} \right] \\ $$$${determine}\:{the}\:{distance}\:{covered} \\ $$$${by}\:{the}\:{body}\:\:{one}\:{hour}\:{after}\: \\ $$$${passing}\:{O}.\:{The}\:{body}\:{moves}\:{along} \\ $$$${a}\:{straight}\:{line}.\:{k},{P},{v}_{{o}} \:{and}\:{m} \\ $$$${are}\:{constants}\:{and}\:{t}\:{is}\:{measured}\:{in} \\ $$$${seconds}. \\ $$$$ \\ $$
Commented by 123456 last updated on 15/Apr/15
![∫_0 ^(3600) (√((1/k)[P−(P−kv_0 ^2 )e^(−((2kt)/m)) ]))dt ∫_0 ^(3600) (√((P/k)−((P−kv_0 ^2 )/k)e^(−((2kt)/m)) ))dt ∫_0 ^(3600) (√(α+βe^(γt) ))dt α=(P/k) β=((kv_0 ^2 −P)/k) γ=−((2k)/m)](https://www.tinkutara.com/question/Q897.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{3600}} {\int}}\sqrt{\frac{\mathrm{1}}{{k}}\left[{P}−\left({P}−{kv}_{\mathrm{0}} ^{\mathrm{2}} \right){e}^{−\frac{\mathrm{2}{kt}}{{m}}} \right]}{dt} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{3600}} {\int}}\sqrt{\frac{{P}}{{k}}−\frac{{P}−{kv}_{\mathrm{0}} ^{\mathrm{2}} }{{k}}{e}^{−\frac{\mathrm{2}{kt}}{{m}}} }{dt} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{3600}} {\int}}\sqrt{\alpha+\beta{e}^{\gamma{t}} }{dt} \\ $$$$\alpha=\frac{{P}}{{k}} \\ $$$$\beta=\frac{{kv}_{\mathrm{0}} ^{\mathrm{2}} −{P}}{{k}} \\ $$$$\gamma=−\frac{\mathrm{2}{k}}{{m}} \\ $$
Commented by prakash jain last updated on 16/Apr/15
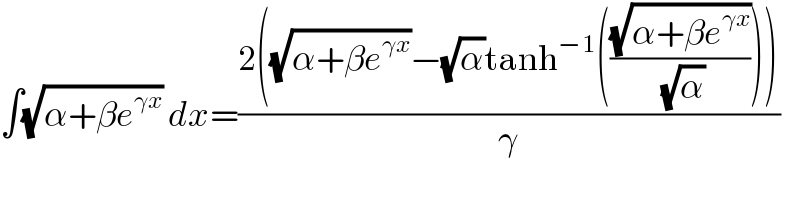
$$\int\sqrt{\alpha+\beta{e}^{\gamma{x}} }\:{dx}=\frac{\mathrm{2}\left(\sqrt{\alpha+\beta{e}^{\gamma{x}} }−\sqrt{\alpha}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\sqrt{\alpha+\beta{e}^{\gamma{x}} }}{\:\sqrt{\alpha}}\right)\right)}{\gamma} \\ $$
