Question Number 70582 by Raphael last updated on 05/Oct/19
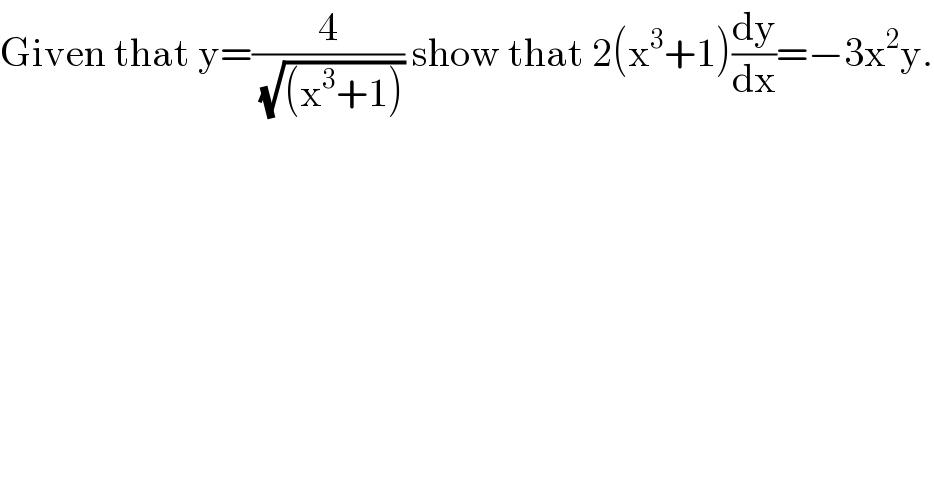
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{y}=\frac{\mathrm{4}}{\:\sqrt{\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)}}\:\mathrm{show}\:\mathrm{that}\:\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)\frac{\mathrm{dy}}{\mathrm{dx}}=−\mathrm{3x}^{\mathrm{2}} \mathrm{y}. \\ $$
Commented by kaivan.ahmadi last updated on 05/Oct/19

$$\mathrm{2}\left({x}^{\mathrm{3}} +\mathrm{1}\right)×\frac{−\frac{\mathrm{4}×\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}}}{{x}^{\mathrm{3}} +\mathrm{1}}=\mathrm{2}×\frac{−\mathrm{2}×\mathrm{3}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}}= \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} ×\frac{\mathrm{4}}{\:\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}}=−\mathrm{3}{x}^{\mathrm{2}} {y} \\ $$
