Question Number 72343 by Rio Michael last updated on 27/Oct/19

$${given}\:{that}\:{y}\:=\:{ln}\:\left(\:\mathrm{1}\:+\:{cos}^{\mathrm{2}} {x}\right)\:{find}\:\frac{{dy}}{{dx}\:\:}\:{at}\:{the}\:{point}\:\:{x}\:=\:\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$${and}\:\:{if}\:\:{y}\:={ln}\left({x}^{\mathrm{2}} \:+\:\mathrm{4}\right)\:{find}\:\:\frac{{dy}}{{dx}}\:{at}\:{x}\:=\:\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 27/Oct/19
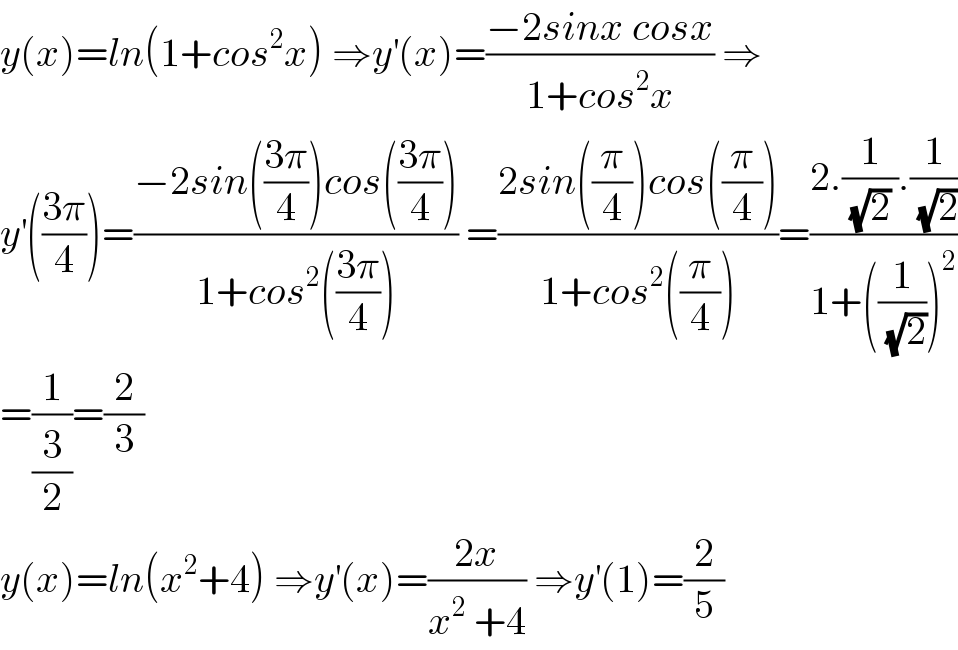
$${y}\left({x}\right)={ln}\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\right)\:\Rightarrow{y}^{'} \left({x}\right)=\frac{−\mathrm{2}{sinx}\:{cosx}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${y}^{'} \left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)=\frac{−\mathrm{2}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right){cos}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)}\:=\frac{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}}\right){cos}\left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\mathrm{2}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${y}\left({x}\right)={ln}\left({x}^{\mathrm{2}} +\mathrm{4}\right)\:\Rightarrow{y}^{'} \left({x}\right)=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow{y}^{'} \left(\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{5}} \\ $$
Commented by Rio Michael last updated on 30/Oct/19

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 31/Oct/19
$${you}\:{are}\:{welcome}. \\ $$
