Given-that-y-n-t-t-B-n-sin-npi-4-t-Evaluate-0-4-y-n-t-2-dt-

Question Number 131315 by Engr_Jidda last updated on 03/Feb/21

Given that y_n (t)=ϱ^t B_n sin((nπ)/4)t Evaluate ∫_0 ^4 [y_n (t)]^2 dt

$${Given}\:{that}\:{y}_{{n}} \left({t}\right)=\varrho^{{t}} {B}_{{n}} {sin}\frac{{n}\pi}{\mathrm{4}}{t} \\ $$$${Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{4}} \left[{y}_{{n}} \left({t}\right)\right]^{\mathrm{2}} {dt} \\ $$

Answered by Ar Brandon last updated on 03/Feb/21

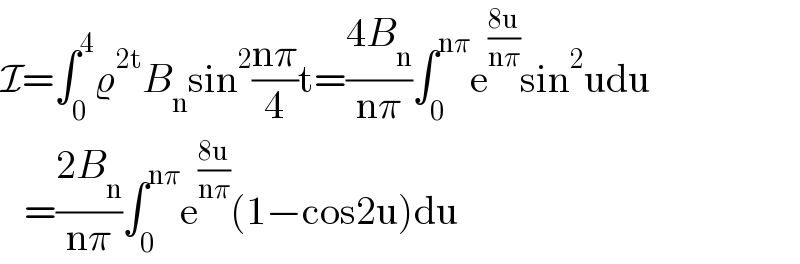
I=∫_0 ^4 ϱ^(2t) B_n sin^2 ((nπ)/4)t=((4B_n )/(nπ))∫_0 ^(nπ) e^((8u)/(nπ)) sin^2 udu =((2B_n )/(nπ))∫_0 ^(nπ) e^((8u)/(nπ)) (1−cos2u)du

$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{4}} \varrho^{\mathrm{2t}} {B}_{\mathrm{n}} \mathrm{sin}^{\mathrm{2}} \frac{\mathrm{n}\pi}{\mathrm{4}}\mathrm{t}=\frac{\mathrm{4}{B}_{\mathrm{n}} }{\mathrm{n}\pi}\int_{\mathrm{0}} ^{\mathrm{n}\pi} \mathrm{e}^{\frac{\mathrm{8u}}{\mathrm{n}\pi}} \mathrm{sin}^{\mathrm{2}} \mathrm{udu} \\ $$$$\:\:\:=\frac{\mathrm{2}{B}_{\mathrm{n}} }{\mathrm{n}\pi}\int_{\mathrm{0}} ^{\mathrm{n}\pi} \mathrm{e}^{\frac{\mathrm{8u}}{\mathrm{n}\pi}} \left(\mathrm{1}−\mathrm{cos2u}\right)\mathrm{du} \\ $$

Commented by Ar Brandon last updated on 03/Feb/21

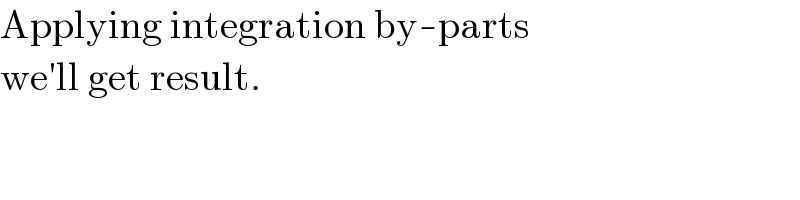
Applying integration by-parts we′ll get result.

$$\mathrm{Applying}\:\mathrm{integration}\:\mathrm{by}-\mathrm{parts}\: \\ $$$$\mathrm{we}'\mathrm{ll}\:\mathrm{get}\:\mathrm{result}. \\ $$

Commented by Engr_Jidda last updated on 03/Feb/21

$${thank}\:{you}\:{sir} \\ $$

Facebook Tweet Pin