Question Number 676 by 123456 last updated on 22/Feb/15
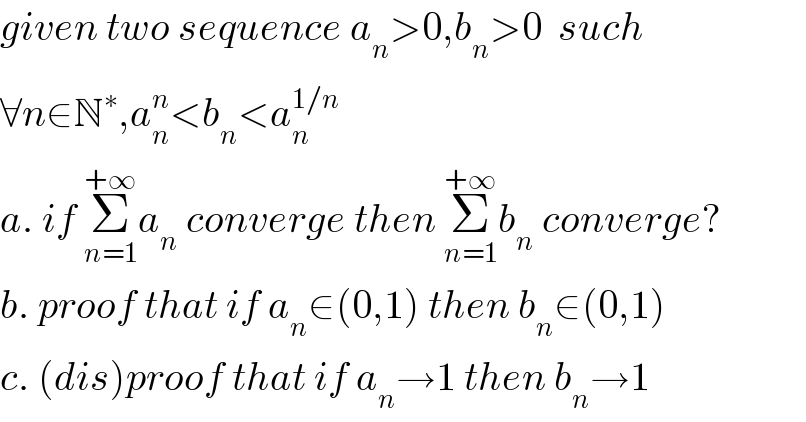
$${given}\:{two}\:{sequence}\:{a}_{{n}} >\mathrm{0},{b}_{{n}} >\mathrm{0}\:\:{such} \\ $$$$\forall{n}\in\mathbb{N}^{\ast} ,{a}_{{n}} ^{{n}} <{b}_{{n}} <{a}_{{n}} ^{\mathrm{1}/{n}} \\ $$$${a}.\:{if}\:\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}{a}_{{n}} \:{converge}\:{then}\:\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}{b}_{{n}} \:{converge}? \\ $$$${b}.\:{proof}\:{that}\:{if}\:{a}_{{n}} \in\left(\mathrm{0},\mathrm{1}\right)\:{then}\:{b}_{{n}} \in\left(\mathrm{0},\mathrm{1}\right) \\ $$$${c}.\:\left({dis}\right){proof}\:{that}\:{if}\:{a}_{{n}} \rightarrow\mathrm{1}\:{then}\:{b}_{{n}} \rightarrow\mathrm{1} \\ $$
Commented by prakash jain last updated on 22/Feb/15
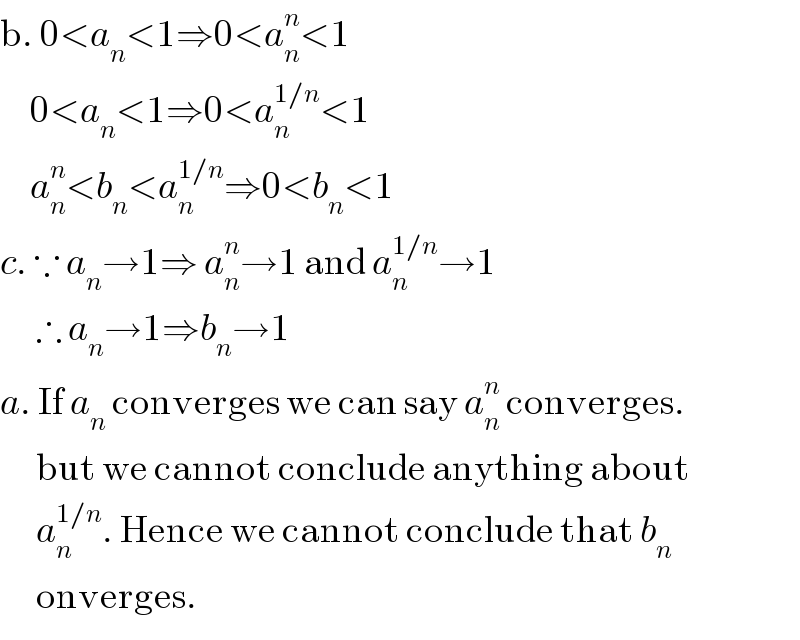
$$\mathrm{b}.\:\mathrm{0}<{a}_{{n}} <\mathrm{1}\Rightarrow\mathrm{0}<{a}_{{n}} ^{{n}} <\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{0}<{a}_{{n}} <\mathrm{1}\Rightarrow\mathrm{0}<{a}_{{n}} ^{\mathrm{1}/{n}} <\mathrm{1} \\ $$$$\:\:\:\:\:{a}_{{n}} ^{{n}} <{b}_{{n}} <{a}_{{n}} ^{\mathrm{1}/{n}} \Rightarrow\mathrm{0}<{b}_{{n}} <\mathrm{1} \\ $$$${c}.\:\because\:{a}_{{n}} \rightarrow\mathrm{1}\Rightarrow\:{a}_{{n}} ^{{n}} \rightarrow\mathrm{1}\:\mathrm{and}\:{a}_{{n}} ^{\mathrm{1}/{n}} \rightarrow\mathrm{1} \\ $$$$\:\:\:\:\:\:\therefore\:{a}_{{n}} \rightarrow\mathrm{1}\Rightarrow{b}_{{n}} \rightarrow\mathrm{1} \\ $$$${a}.\:\mathrm{If}\:{a}_{{n}} \:\mathrm{converges}\:\mathrm{we}\:\mathrm{can}\:\mathrm{say}\:{a}_{{n}} ^{{n}} \:\mathrm{converges}. \\ $$$$\:\:\:\:\:\:\mathrm{but}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{conclude}\:\mathrm{anything}\:\mathrm{about} \\ $$$$\:\:\:\:\:\:{a}_{{n}} ^{\mathrm{1}/{n}} .\:\mathrm{Hence}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{conclude}\:\mathrm{that}\:{b}_{{n}} \\ $$$$\:\:\:\:\:\:\mathrm{onverges}.\: \\ $$
