Question Number 135418 by liberty last updated on 13/Mar/21
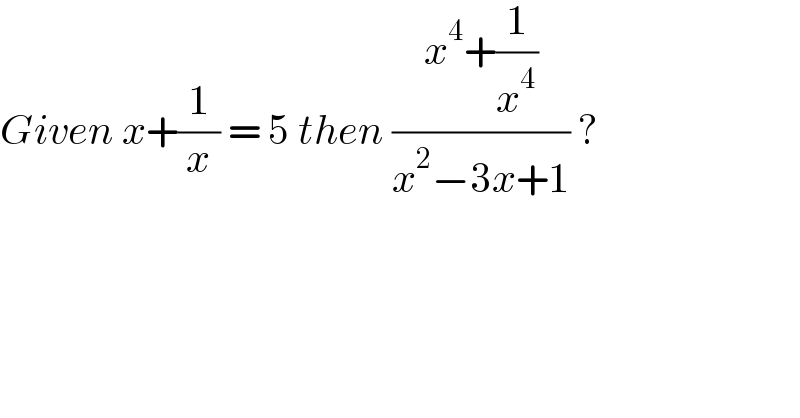
$${Given}\:{x}+\frac{\mathrm{1}}{{x}}\:=\:\mathrm{5}\:{then}\:\frac{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}}\:? \\ $$
Answered by SEKRET last updated on 13/Mar/21
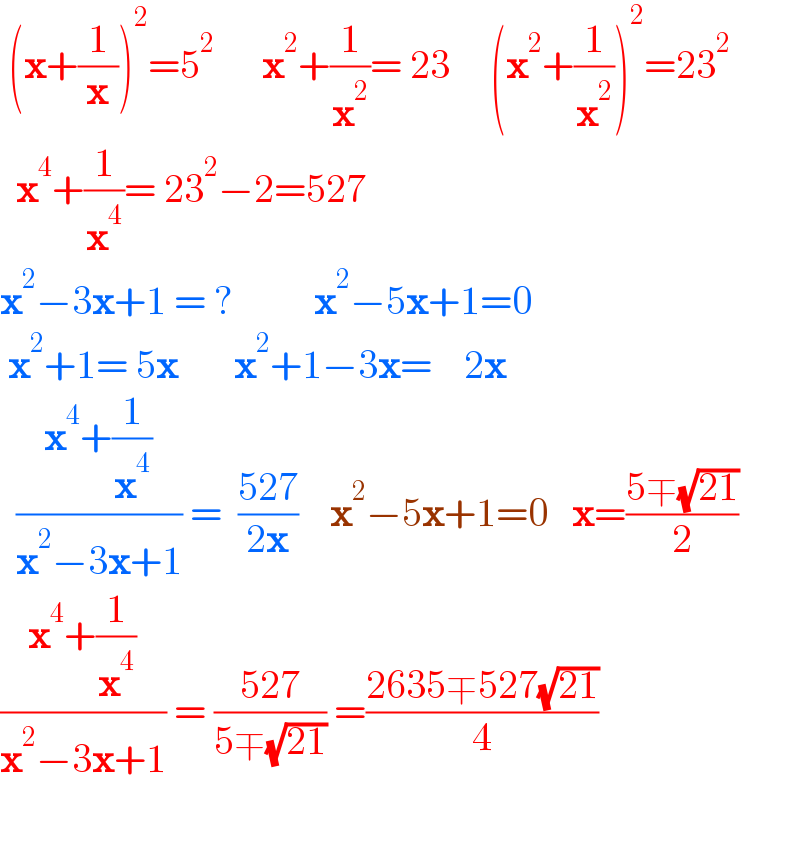
$$\:\left(\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\:\mathrm{23}\:\:\:\:\:\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{23}^{\mathrm{2}} \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} }=\:\mathrm{23}^{\mathrm{2}} −\mathrm{2}=\mathrm{527} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{1}\:=\:?\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=\:\mathrm{5}\boldsymbol{\mathrm{x}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}−\mathrm{3}\boldsymbol{\mathrm{x}}=\:\:\:\:\mathrm{2}\boldsymbol{\mathrm{x}} \\ $$$$\:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} }}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{1}}\:=\:\:\frac{\mathrm{527}}{\mathrm{2}\boldsymbol{\mathrm{x}}}\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{\mathrm{x}}+\mathrm{1}=\mathrm{0}\:\:\:\boldsymbol{\mathrm{x}}=\frac{\mathrm{5}\mp\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\frac{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} }}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{\mathrm{x}}+\mathrm{1}}\:=\:\frac{\mathrm{527}}{\mathrm{5}\mp\sqrt{\mathrm{21}}}\:=\frac{\mathrm{2635}\mp\mathrm{527}\sqrt{\mathrm{21}}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Ñï= last updated on 13/Mar/21
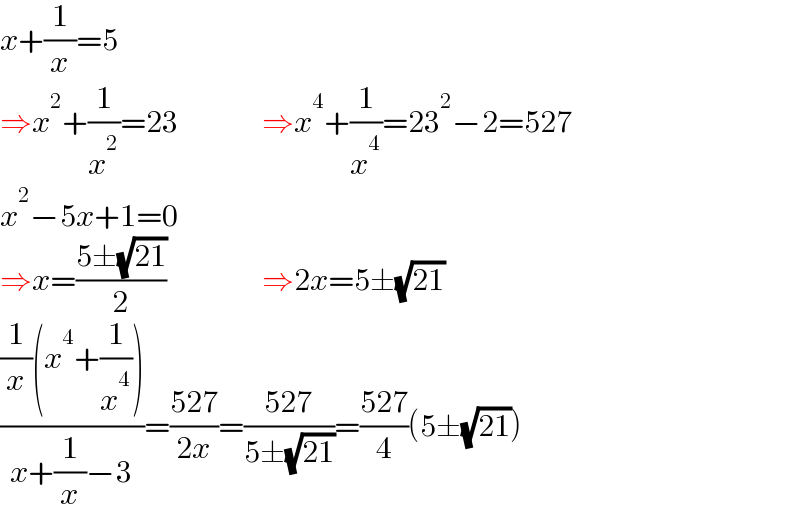
$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{5} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{23}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }=\mathrm{23}^{\mathrm{2}} −\mathrm{2}=\mathrm{527} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{21}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{2}{x}=\mathrm{5}\pm\sqrt{\mathrm{21}} \\ $$$$\frac{\frac{\mathrm{1}}{{x}}\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)}{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{3}}=\frac{\mathrm{527}}{\mathrm{2}{x}}=\frac{\mathrm{527}}{\mathrm{5}\pm\sqrt{\mathrm{21}}}=\frac{\mathrm{527}}{\mathrm{4}}\left(\mathrm{5}\pm\sqrt{\mathrm{21}}\right) \\ $$
