Question Number 74024 by ajfour last updated on 18/Nov/19
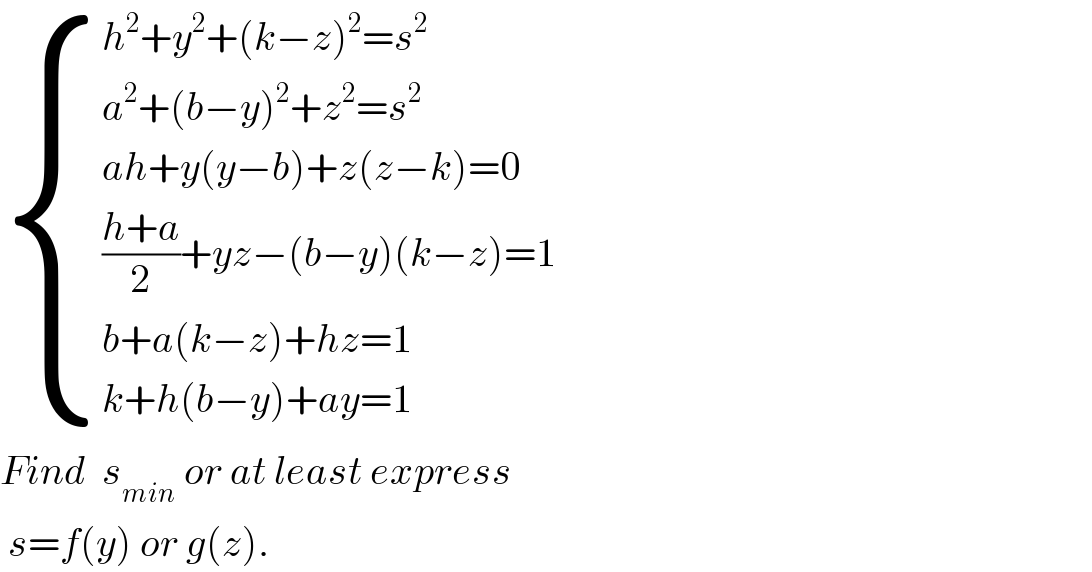
$$\begin{cases}{{h}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({k}−{z}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} }\\{{a}^{\mathrm{2}} +\left({b}−{y}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} ={s}^{\mathrm{2}} }\\{{ah}+{y}\left({y}−{b}\right)+{z}\left({z}−{k}\right)=\mathrm{0}}\\{\frac{{h}+{a}}{\mathrm{2}}+{yz}−\left({b}−{y}\right)\left({k}−{z}\right)=\mathrm{1}}\\{{b}+{a}\left({k}−{z}\right)+{hz}=\mathrm{1}}\\{{k}+{h}\left({b}−{y}\right)+{ay}=\mathrm{1}}\end{cases} \\ $$$${Find}\:\:{s}_{{min}} \:{or}\:{at}\:{least}\:{express} \\ $$$$\:{s}={f}\left({y}\right)\:{or}\:{g}\left({z}\right). \\ $$
Commented by mind is power last updated on 18/Nov/19
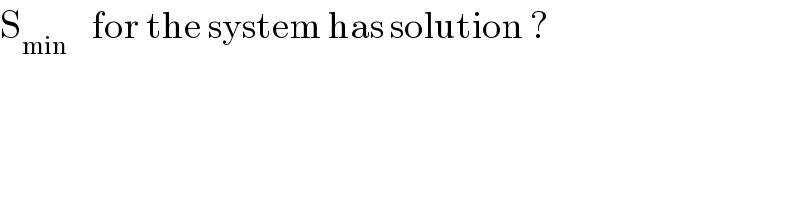
$$\mathrm{S}_{\mathrm{min}\:\:\:} \:\:\mathrm{for}\:\mathrm{the}\:\mathrm{system}\:\mathrm{has}\:\mathrm{solution}\:? \\ $$
Answered by ajfour last updated on 18/Nov/19
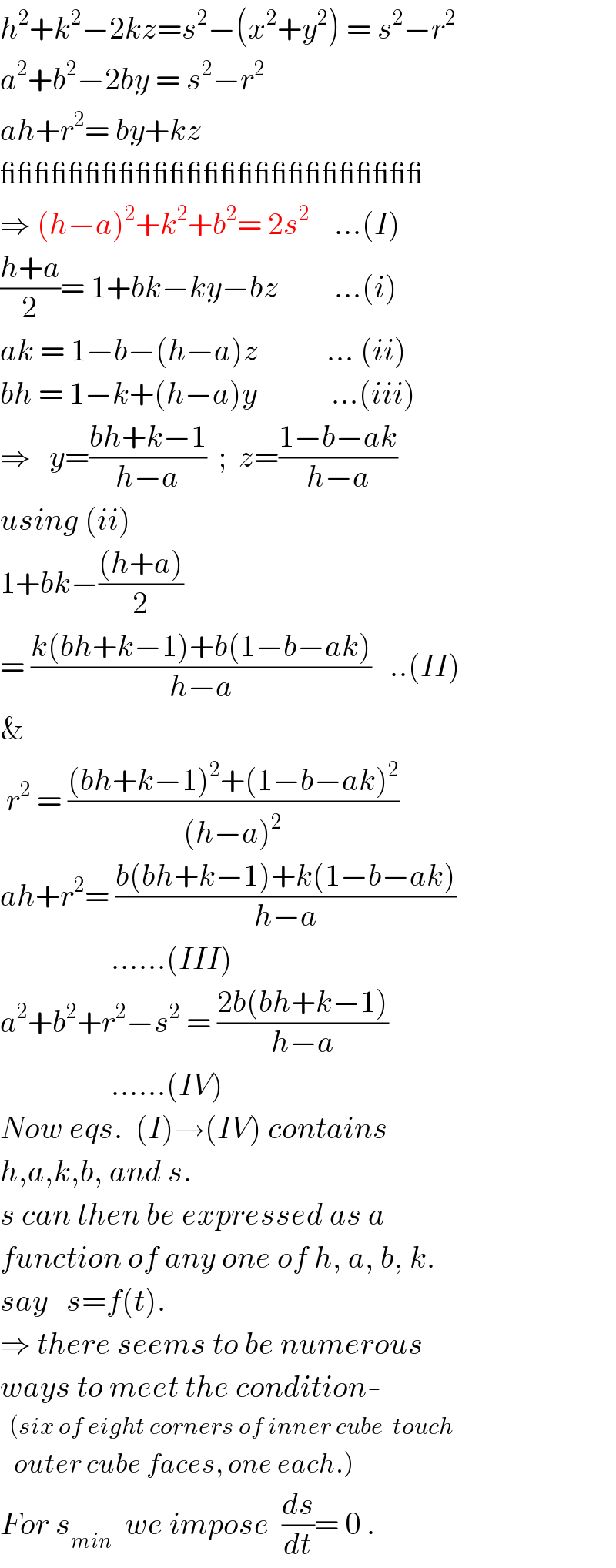
$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\mathrm{2}{kz}={s}^{\mathrm{2}} −\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:=\:{s}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{by}\:=\:{s}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${ah}+{r}^{\mathrm{2}} =\:{by}+{kz}\:\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\left({h}−{a}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} +{b}^{\mathrm{2}} =\:\mathrm{2}{s}^{\mathrm{2}} \:\:\:\:…\left({I}\right) \\ $$$$\frac{{h}+{a}}{\mathrm{2}}=\:\mathrm{1}+{bk}−{ky}−{bz}\:\:\:\:\:\:\:\:\:…\left({i}\right) \\ $$$${ak}\:=\:\mathrm{1}−{b}−\left({h}−{a}\right){z}\:\:\:\:\:\:\:\:\:\:\:…\:\left({ii}\right) \\ $$$${bh}\:=\:\mathrm{1}−{k}+\left({h}−{a}\right){y}\:\:\:\:\:\:\:\:\:\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\:\:\:{y}=\frac{{bh}+{k}−\mathrm{1}}{{h}−{a}}\:\:;\:\:{z}=\frac{\mathrm{1}−{b}−{ak}}{{h}−{a}} \\ $$$${using}\:\left({ii}\right) \\ $$$$\mathrm{1}+{bk}−\frac{\left({h}+{a}\right)}{\mathrm{2}}\: \\ $$$$=\:\frac{{k}\left({bh}+{k}−\mathrm{1}\right)+{b}\left(\mathrm{1}−{b}−{ak}\right)}{{h}−{a}}\:\:\:..\left({II}\right) \\ $$$$\& \\ $$$$\:{r}^{\mathrm{2}} \:=\:\frac{\left({bh}+{k}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}−{b}−{ak}\right)^{\mathrm{2}} }{\left({h}−{a}\right)^{\mathrm{2}} } \\ $$$${ah}+{r}^{\mathrm{2}} =\:\frac{{b}\left({bh}+{k}−\mathrm{1}\right)+{k}\left(\mathrm{1}−{b}−{ak}\right)}{{h}−{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……\left({III}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{r}^{\mathrm{2}} −{s}^{\mathrm{2}} \:=\:\frac{\mathrm{2}{b}\left({bh}+{k}−\mathrm{1}\right)}{{h}−{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……\left({IV}\right) \\ $$$${Now}\:{eqs}.\:\:\left({I}\right)\rightarrow\left({IV}\right)\:{contains} \\ $$$${h},{a},{k},{b},\:{and}\:{s}.\:\: \\ $$$${s}\:{can}\:{then}\:{be}\:{expressed}\:{as}\:{a}\: \\ $$$${function}\:{of}\:{any}\:{one}\:{of}\:{h},\:{a},\:{b},\:{k}. \\ $$$${say}\:\:\:{s}={f}\left({t}\right). \\ $$$$\Rightarrow\:{there}\:{seems}\:{to}\:{be}\:{numerous} \\ $$$${ways}\:{to}\:{meet}\:{the}\:{condition}- \\ $$$$\:\:\left({six}\:{of}\:{eight}\:{corners}\:{of}\:{inner}\:{cube}\:\:{touch}\:\right. \\ $$$$\left.\:\:\:{outer}\:{cube}\:{faces},\:{one}\:{each}.\right) \\ $$$${For}\:{s}_{{min}} \:\:{we}\:{impose}\:\:\frac{{ds}}{{dt}}=\:\mathrm{0}\:. \\ $$
