Hello-i-shar-withe-you-nice-problem-show-that-k-N-n-N-such-that-k-j-1-n-1-j-lt-k-1-have-a-very-Nice-day-

Question Number 73378 by mind is power last updated on 10/Nov/19

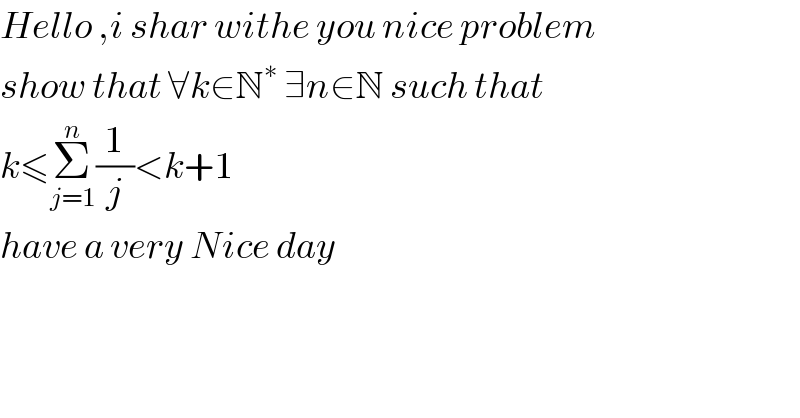
H e l l o, i s h a r w i t h e y o u n i c e p r o b l e m

s h o w t h a t \forall k \in N^{*} \exists n \in N s u c h t h a t

k ⩽ \underset{j = 1}{\sum^{n}} \frac{1}{j} < k + 1

h a v e a v e r y N i c e d a y

Commented by MJS last updated on 11/Nov/19

H_{n} = \underset{j = 1}{\sum^{n}} \frac{1}{j}; \lim_{n \to + \infty} H_{n} = + \infty

\forall n \in N : {\begin{cases} H_{n + 1} - H_{n} < 1 \\ H_{n + 2} - H_{n + 1} < H_{n + 1} - H_{n} \end{cases}

k = 1

1 ⩽ H_{1} < H_{2} < H_{3} < 2

\Rightarrow \forall k \in N^{★} \exists n \in N : k ⩽ \underset{j = 1}{\sum^{n}} \frac{1}{j} < k + 1

Commented by mind is power last updated on 11/Nov/19

n i c e s o l u t i o n

Commented by MJS last updated on 11/Nov/19

thank you

Facebook Tweet Pin