Question Number 76477 by mathocean1 last updated on 27/Dec/19
![Hello Solve in ]−π;π[ ((2sinx)/(cosx−sinx))≥0 result should be in radian please help me ...](https://www.tinkutara.com/question/Q76477.png)
Answered by Kunal12588 last updated on 27/Dec/19
![((2sin x)/(cos x−sin x))=(((√2)sin x)/(sin((π/4)−x)))≥0 ⇒x∈[0,(π/4))∪(−((3π)/4),−π]](https://www.tinkutara.com/question/Q76478.png)
Commented by mathocean1 last updated on 27/Dec/19
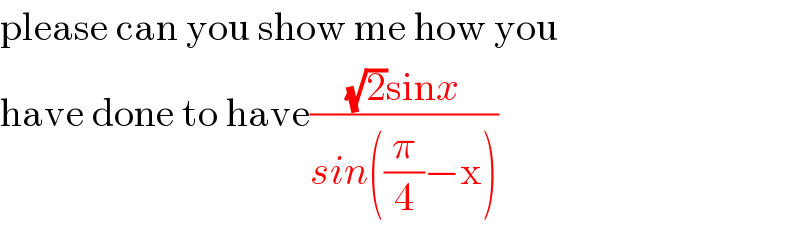
Commented by Kunal12588 last updated on 27/Dec/19
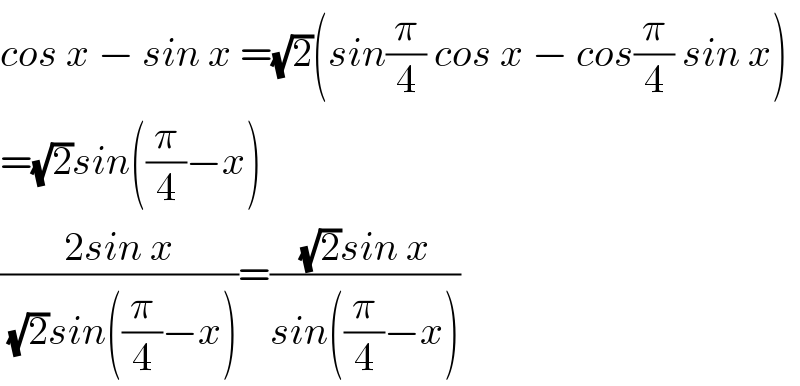
Commented by mathocean1 last updated on 27/Dec/19
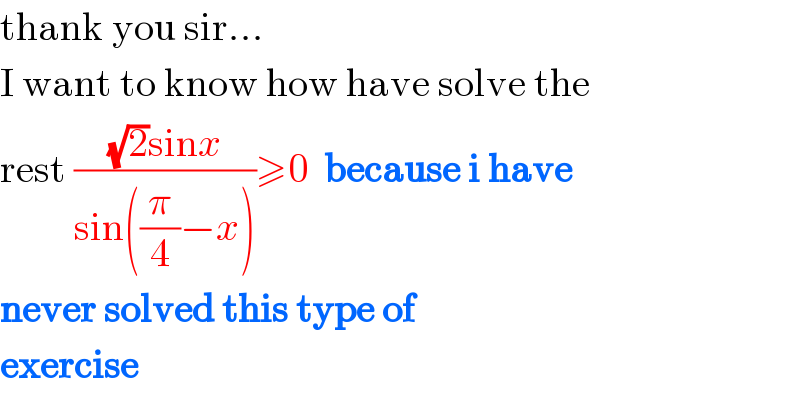
Commented by Kunal12588 last updated on 27/Dec/19

Commented by mathocean1 last updated on 27/Dec/19

Answered by MJS last updated on 27/Dec/19
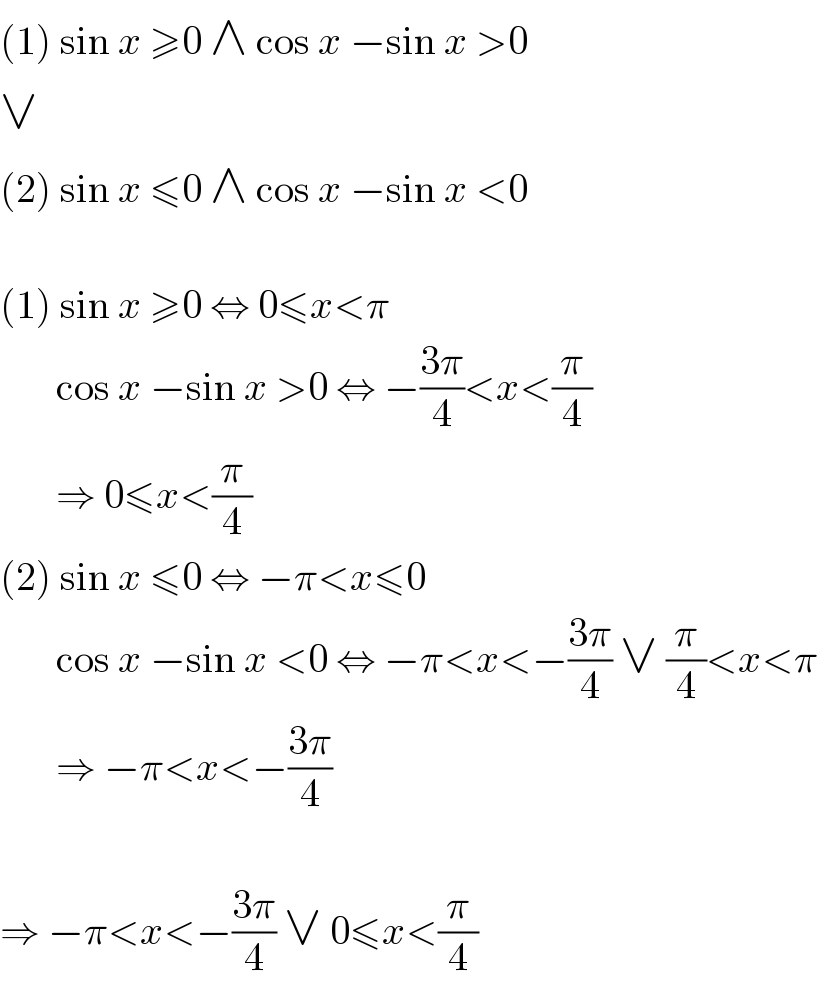
Commented by mr W last updated on 28/Dec/19

Commented by MJS last updated on 28/Dec/19
![he typed ]−π; π[ ⇔ −π<x<π](https://www.tinkutara.com/question/Q76552.png)
