Question Number 135459 by Abdoulaye last updated on 13/Mar/21
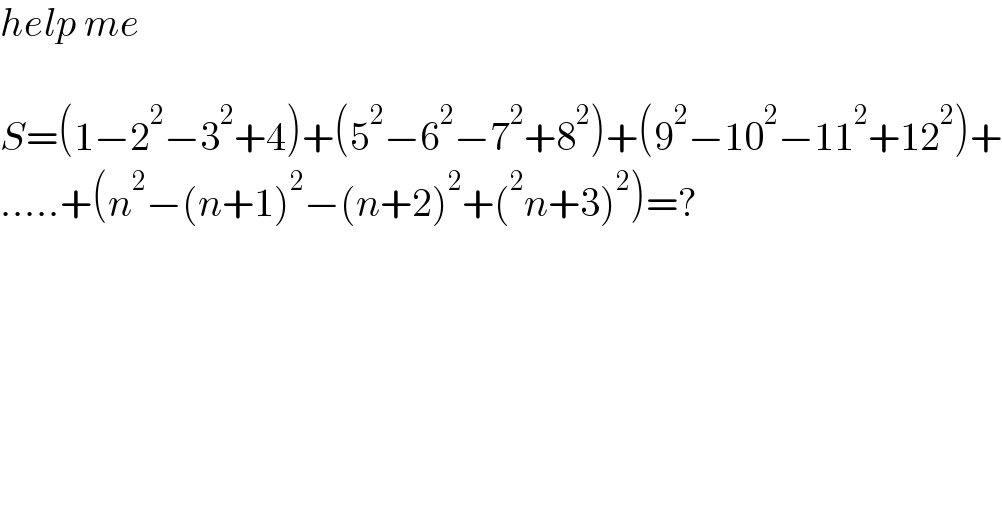
$${help}\:{me} \\ $$$$ \\ $$$${S}=\left(\mathrm{1}−\mathrm{2}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} +\mathrm{4}\right)+\left(\mathrm{5}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} \right)+\left(\mathrm{9}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} −\mathrm{11}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} \right)+ \\ $$$$…..+\left({n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)^{\mathrm{2}} +\left(^{\mathrm{2}} {n}+\mathrm{3}\right)^{\mathrm{2}} \right)=? \\ $$
Answered by mr W last updated on 13/Mar/21
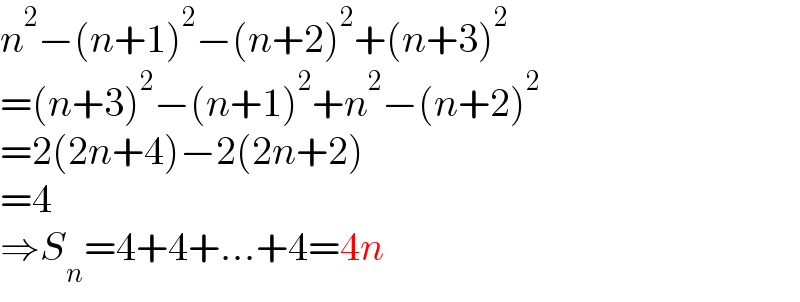
$${n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)^{\mathrm{2}} +\left({n}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$=\left({n}+\mathrm{3}\right)^{\mathrm{2}} −\left({n}+\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} −\left({n}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\mathrm{2}{n}+\mathrm{4}\right)−\mathrm{2}\left(\mathrm{2}{n}+\mathrm{2}\right) \\ $$$$=\mathrm{4} \\ $$$$\Rightarrow{S}_{{n}} =\mathrm{4}+\mathrm{4}+…+\mathrm{4}=\mathrm{4}{n} \\ $$
Commented by Abdoulaye last updated on 13/Mar/21

$${thank}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 13/Mar/21
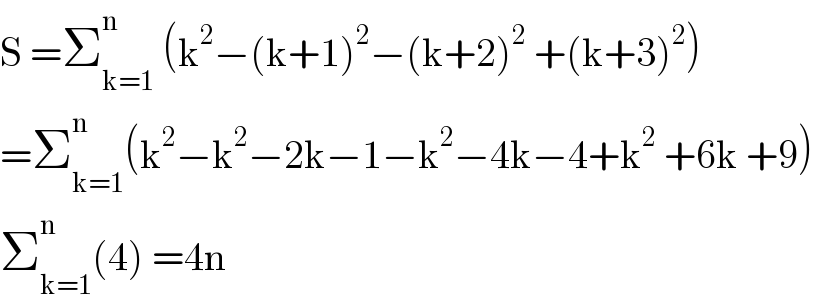
$$\mathrm{S}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\mathrm{k}^{\mathrm{2}} −\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{k}+\mathrm{2}\right)^{\mathrm{2}} \:+\left(\mathrm{k}+\mathrm{3}\right)^{\mathrm{2}} \right) \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{k}^{\mathrm{2}} −\mathrm{k}^{\mathrm{2}} −\mathrm{2k}−\mathrm{1}−\mathrm{k}^{\mathrm{2}} −\mathrm{4k}−\mathrm{4}+\mathrm{k}^{\mathrm{2}} \:+\mathrm{6k}\:+\mathrm{9}\right) \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{4}\right)\:=\mathrm{4n} \\ $$
