Question Number 10417 by okhema francis last updated on 08/Feb/17

$${hence}\:{or}\:{other}\mathrm{wise}\:\mathrm{solve}\:\mathrm{sin}\:\mathrm{6}\theta−\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0}\:{for}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}. \\ $$$$ \\ $$
Answered by nume1114 last updated on 08/Feb/17
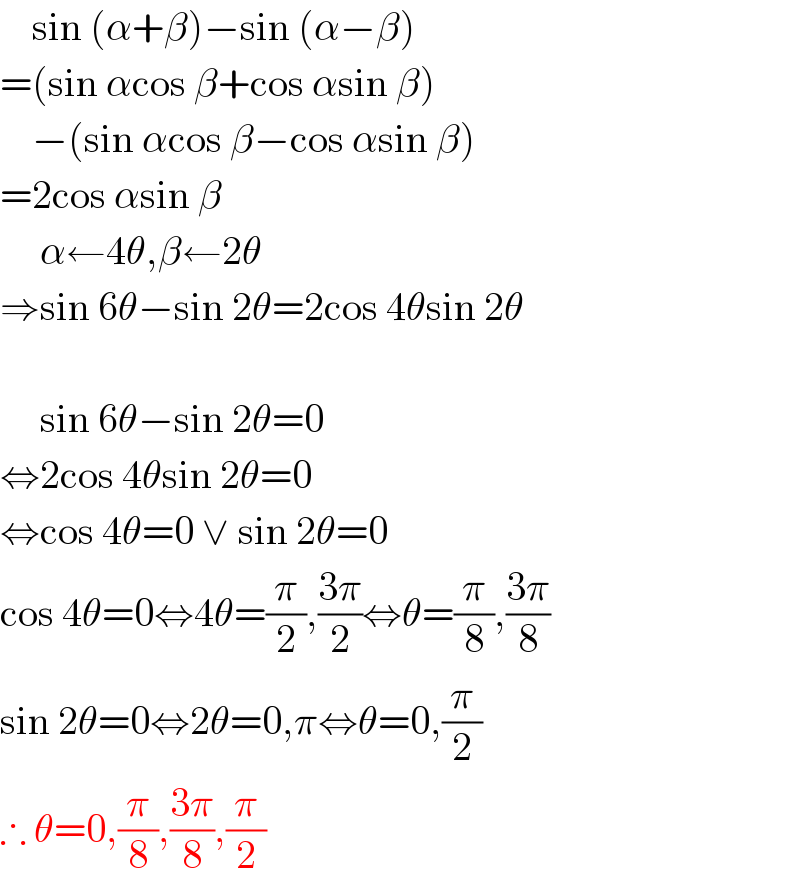
$$\:\:\:\:\mathrm{sin}\:\left(\alpha+\beta\right)−\mathrm{sin}\:\left(\alpha−\beta\right) \\ $$$$=\left(\mathrm{sin}\:\alpha\mathrm{cos}\:\beta+\mathrm{cos}\:\alpha\mathrm{sin}\:\beta\right) \\ $$$$\:\:\:\:−\left(\mathrm{sin}\:\alpha\mathrm{cos}\:\beta−\mathrm{cos}\:\alpha\mathrm{sin}\:\beta\right) \\ $$$$=\mathrm{2cos}\:\alpha\mathrm{sin}\:\beta \\ $$$$\:\:\:\:\:\alpha\leftarrow\mathrm{4}\theta,\beta\leftarrow\mathrm{2}\theta \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{6}\theta−\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2cos}\:\mathrm{4}\theta\mathrm{sin}\:\mathrm{2}\theta \\ $$$$ \\ $$$$\:\:\:\:\:\mathrm{sin}\:\mathrm{6}\theta−\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2cos}\:\mathrm{4}\theta\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{cos}\:\mathrm{4}\theta=\mathrm{0}\:\vee\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=\mathrm{0}\Leftrightarrow\mathrm{4}\theta=\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}}\Leftrightarrow\theta=\frac{\pi}{\mathrm{8}},\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0}\Leftrightarrow\mathrm{2}\theta=\mathrm{0},\pi\Leftrightarrow\theta=\mathrm{0},\frac{\pi}{\mathrm{2}} \\ $$$$\therefore\:\theta=\mathrm{0},\frac{\pi}{\mathrm{8}},\frac{\mathrm{3}\pi}{\mathrm{8}},\frac{\pi}{\mathrm{2}} \\ $$
Commented by okhema francis last updated on 09/Feb/17

$${thank}\:{you}\:{and}\:{let}\:{the}\:{lord}\:{be}\:{with}\:{u} \\ $$
Answered by mrW1 last updated on 08/Feb/17
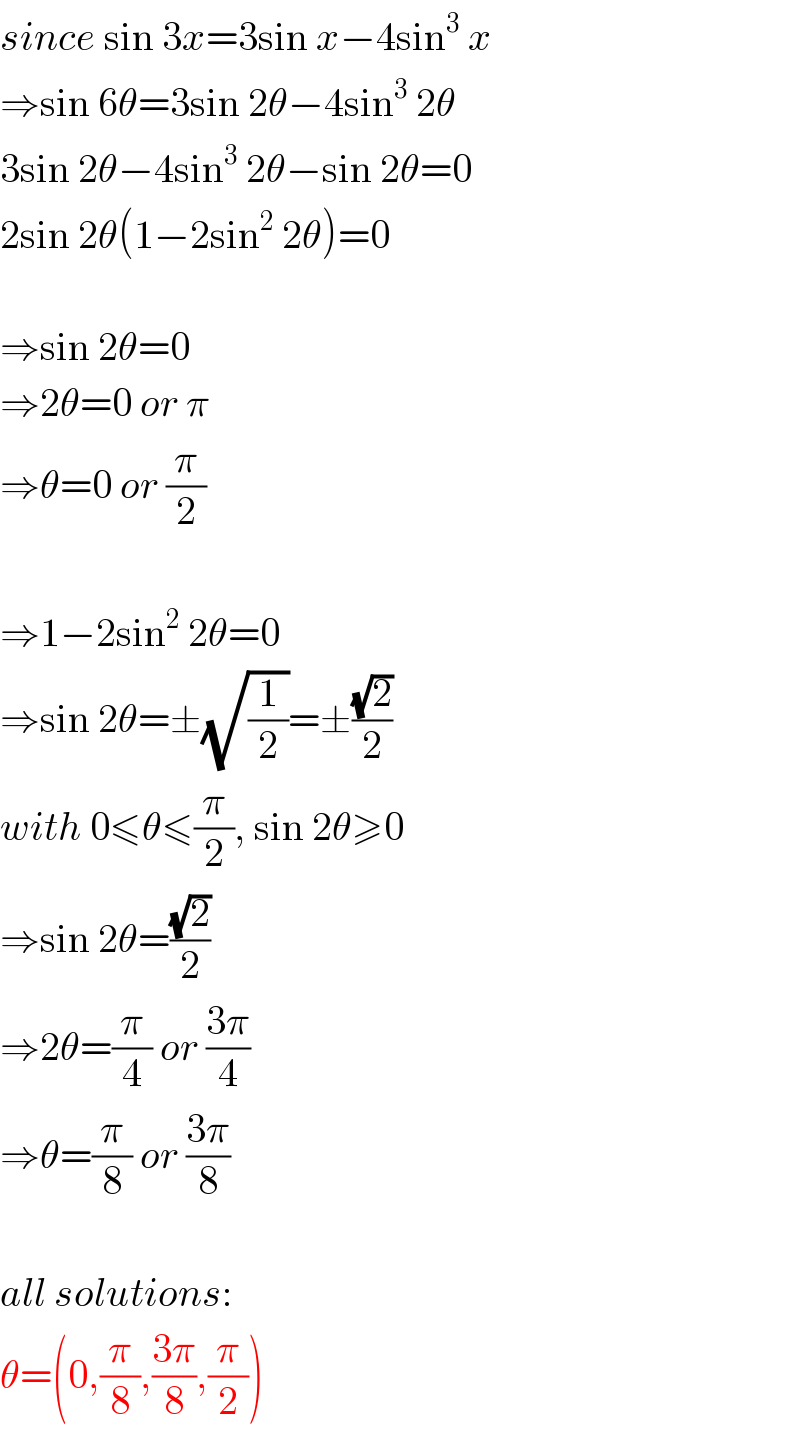
$${since}\:\mathrm{sin}\:\mathrm{3}{x}=\mathrm{3sin}\:{x}−\mathrm{4sin}^{\mathrm{3}} \:{x} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{6}\theta=\mathrm{3sin}\:\mathrm{2}\theta−\mathrm{4sin}^{\mathrm{3}} \:\mathrm{2}\theta \\ $$$$\mathrm{3sin}\:\mathrm{2}\theta−\mathrm{4sin}^{\mathrm{3}} \:\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\mathrm{2sin}\:\mathrm{2}\theta\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\mathrm{2}\theta\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\theta=\mathrm{0}\:{or}\:\pi \\ $$$$\Rightarrow\theta=\mathrm{0}\:{or}\:\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\pm\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${with}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}},\:\mathrm{sin}\:\mathrm{2}\theta\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\theta=\frac{\pi}{\mathrm{4}}\:{or}\:\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{8}}\:{or}\:\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$ \\ $$$${all}\:{solutions}: \\ $$$$\theta=\left(\mathrm{0},\frac{\pi}{\mathrm{8}},\frac{\mathrm{3}\pi}{\mathrm{8}},\frac{\pi}{\mathrm{2}}\right) \\ $$
Commented by okhema francis last updated on 09/Feb/17
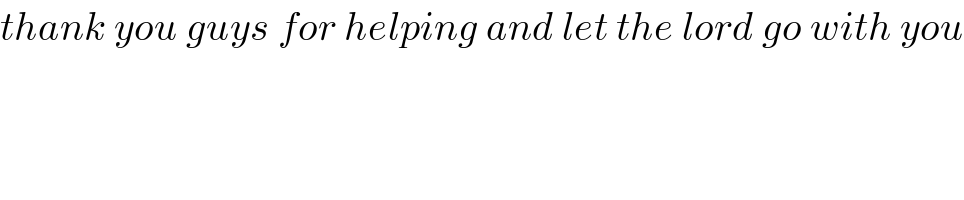
$${thank}\:{you}\:{guys}\:{for}\:{helping}\:{and}\:{let}\:{the}\:{lord}\:{go}\:{with}\:{you} \\ $$
