Question Number 1676 by hhhggvghhh last updated on 31/Aug/15

$$\boldsymbol{{hhjghhjjgkggjggigfhpppkknbgjffffg}} \\ $$$$\boldsymbol{{biuggjnggtbnkoyfhjiuhbhuklphh}} \\ $$$$\boldsymbol{{jinbh}}\mathrm{678656}\boldsymbol{{kkiohhuggjngffjkkdooxk}} \\ $$$$\boldsymbol{{ikhhkjhv}}\mathrm{2}\left[\mathrm{65}\sqrt{\sqrt{\mathrm{58}\:\mathrm{889}<\boldsymbol{{lkkjkbmbbnnb}}}}\right. \\ $$$$\boldsymbol{{jkkhjm}}\sqrt{\boldsymbol{{nlm}}\mathrm{6}\boldsymbol{{jikmbh}}\sqrt{\boldsymbol{{jlbj}}}} \\ $$$$\boldsymbol{{jljbnkbbnmnmmnjknbjnrurubv}}\underset{\boldsymbol{{nkjnbmm}}} {\boldsymbol{{m}}} \\ $$$$\boldsymbol{{jjnbbnjnnj}}^{} \\ $$$$\boldsymbol{{nkn}} \\ $$$$ \\ $$$$\boldsymbol{{mkknjlmmK}}{ihkhjZzz}\theta{n}\mathrm{5}\psi{n}\mathrm{6} \\ $$
Commented by 123456 last updated on 31/Aug/15

$$\mathrm{XD} \\ $$
Commented by Rasheed Ahmad last updated on 01/Sep/15
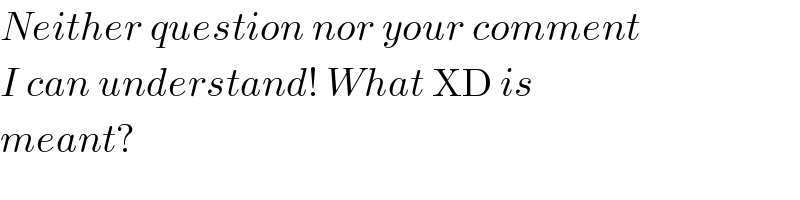
$${Neither}\:{question}\:{nor}\:{your}\:{comment} \\ $$$${I}\:{can}\:{understand}!\:{What}\:\mathrm{XD}\:{is} \\ $$$${meant}? \\ $$
Commented by 123456 last updated on 01/Sep/15

$$\mathrm{a}\:\mathrm{happy}\:\mathrm{face} \\ $$
Answered by 123456 last updated on 31/Aug/15

$$\underset{{x}\rightarrow{a}^{+} } {\mathrm{lim}}{f}\left({x}\right)=\mathrm{L} \\ $$$$\forall\epsilon>\mathrm{0},\exists\delta,\mathrm{0}<{x}−{a}<\delta,\mid{f}\left({x}\right)−\mathrm{L}\mid<\epsilon \\ $$
Answered by Yozzy last updated on 31/Aug/15
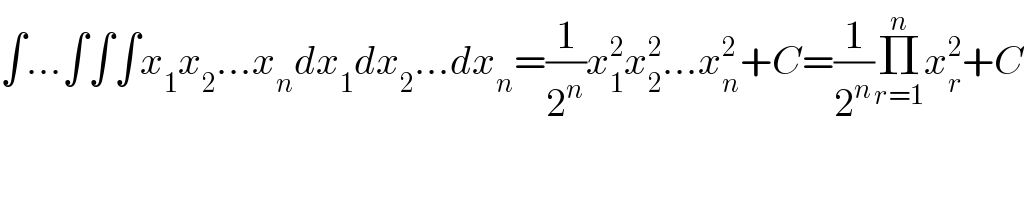
$$\int…\int\int\int{x}_{\mathrm{1}} {x}_{\mathrm{2}} …{x}_{{n}} {dx}_{\mathrm{1}} {dx}_{\mathrm{2}} …{dx}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }{x}_{\mathrm{1}} ^{\mathrm{2}} {x}_{\mathrm{2}} ^{\mathrm{2}} …{x}_{{n}} ^{\mathrm{2}} +{C}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}{x}_{{r}} ^{\mathrm{2}} +{C} \\ $$
Answered by 123456 last updated on 31/Aug/15
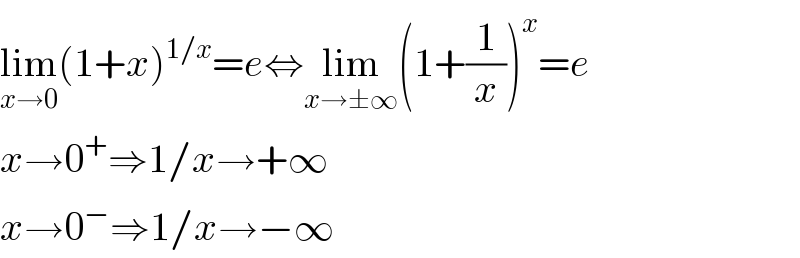
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} ={e}\Leftrightarrow\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} ={e} \\ $$$${x}\rightarrow\mathrm{0}^{+} \Rightarrow\mathrm{1}/{x}\rightarrow+\infty \\ $$$${x}\rightarrow\mathrm{0}^{−} \Rightarrow\mathrm{1}/{x}\rightarrow−\infty \\ $$
