Question Number 138257 by greg_ed last updated on 11/Apr/21
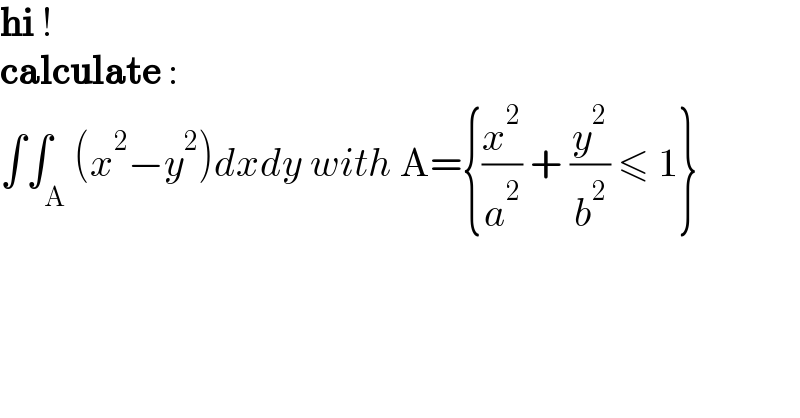
$$\boldsymbol{\mathrm{hi}}\:! \\ $$$$\boldsymbol{\mathrm{calculate}}\::\: \\ $$$$\int\int_{\mathrm{A}} \left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){dxdy}\:{with}\:\mathrm{A}=\left\{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\:\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\leqslant\:\mathrm{1}\right\} \\ $$
Answered by mathmax by abdo last updated on 11/Apr/21
![we consider the diffeomorphism { ((x=arcosθ)),((y=brsinθ)) :} (x^2 /a^2 )+(y^2 /b^2 ) =r^2 (cos^2 θ+sin^2 θ)=r^2 ≤1 ⇒o≤r≤1 ∫∫ (x^2 −y^2 )dxdy =∫_(0≤r<1) ∫_0 ^(2π) (a^2 r^2 cos^2 θ−b^2 r^2 sin^2 θ)abrdrdθ =ab ∫_0 ^1 r^3 dr∫_0 ^(2π) (a^2 cos^2 θ−b^2 sin^2 θ)dθ but ∫_0 ^1 r^3 dr=[(r^4 /4)]_0 ^1 =(1/4) ∫_0 ^(2π) (a^2 cos^2 θ−b^2 sin^2 θ)dθ =(a^2 /2)∫_0 ^(2π) (1+cos(2θ))dθ −(b^2 /2)∫_0 ^(2π) (1−cos(2θ))dθ =πa^2 +(a^2 /4)[sin(2θ)]_0 ^(2π) −πb^2 +(b^2 /2)[sin(2θ)]_0 ^(2π) =πa^2 +0−πb^2 +0 =π(a^2 −b^2 ) ⇒ ∫∫_A (x^2 −y^2 )dxdy =((ab)/4).π(a^2 −b^2 )=(π/4)(a^3 b−ab^3 )](https://www.tinkutara.com/question/Q138268.png)
$$\mathrm{we}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{diffeomorphism}\:\:\begin{cases}{\mathrm{x}=\mathrm{arcos}\theta}\\{\mathrm{y}=\mathrm{brsin}\theta}\end{cases} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }\:=\mathrm{r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right)=\mathrm{r}^{\mathrm{2}} \leqslant\mathrm{1}\:\Rightarrow\mathrm{o}\leqslant\mathrm{r}\leqslant\mathrm{1} \\ $$$$\int\int\:\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)\mathrm{dxdy}\:=\int_{\mathrm{0}\leqslant\mathrm{r}<\mathrm{1}} \:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{a}^{\mathrm{2}} \mathrm{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta−\mathrm{b}^{\mathrm{2}} \mathrm{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\right)\mathrm{abrdrd}\theta \\ $$$$=\mathrm{ab}\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{r}^{\mathrm{3}} \:\mathrm{dr}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta−\mathrm{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\right)\mathrm{d}\theta\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{r}^{\mathrm{3}} \mathrm{dr}=\left[\frac{\mathrm{r}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta−\mathrm{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\right)\mathrm{d}\theta\:=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta \\ $$$$−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{d}\theta\:=\pi\mathrm{a}^{\mathrm{2}} \:+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$−\pi\mathrm{b}^{\mathrm{2}} \:+\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}\left[\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:=\pi\mathrm{a}^{\mathrm{2}} +\mathrm{0}−\pi\mathrm{b}^{\mathrm{2}} \:+\mathrm{0}\:=\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\int\int_{\mathrm{A}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)\mathrm{dxdy}\:=\frac{\mathrm{ab}}{\mathrm{4}}.\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)=\frac{\pi}{\mathrm{4}}\left(\mathrm{a}^{\mathrm{3}} \mathrm{b}−\mathrm{ab}^{\mathrm{3}} \right) \\ $$$$ \\ $$
Commented by greg_ed last updated on 11/Apr/21
$$\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{much}},\:\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{friend}}\:\boldsymbol{\mathrm{mathmax}}\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{abdo}}\:! \\ $$
Commented by mathmax by abdo last updated on 12/Apr/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$
