Question Number 138473 by henderson last updated on 14/Apr/21
![hi ! calculate : lim_(x→∞) [((ln(x+1))/(ln (x)))]^(x ln (x)) .](https://www.tinkutara.com/question/Q138473.png)
$$\boldsymbol{\mathrm{hi}}\:! \\ $$$$\boldsymbol{\mathrm{calculate}}\::\:\underset{{x}\rightarrow\infty} {{lim}}\:\left[\frac{{ln}\left({x}+\mathrm{1}\right)}{{ln}\:\left({x}\right)}\right]^{{x}\:{ln}\:\left({x}\right)} . \\ $$
Answered by mathmax by abdo last updated on 14/Apr/21
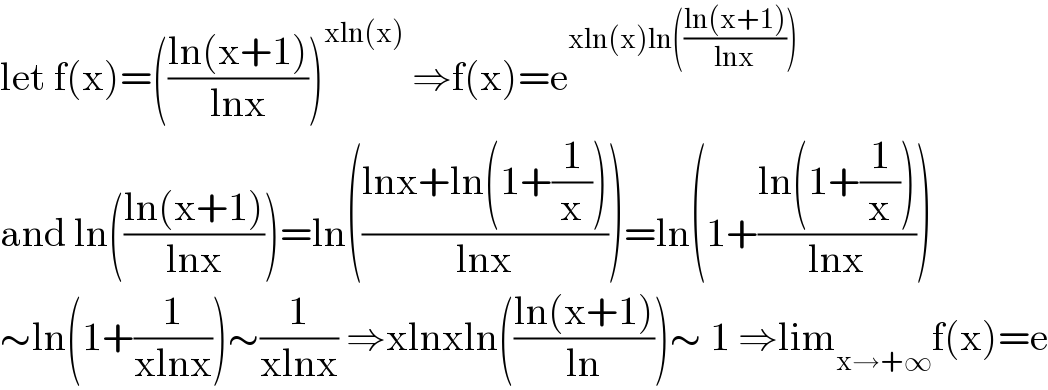
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{lnx}}\right)^{\mathrm{xln}\left(\mathrm{x}\right)} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{xln}\left(\mathrm{x}\right)\mathrm{ln}\left(\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{lnx}}\right)} \\ $$$$\mathrm{and}\:\mathrm{ln}\left(\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{lnx}}\right)=\mathrm{ln}\left(\frac{\mathrm{lnx}+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{lnx}}\right)=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{lnx}}\right) \\ $$$$\sim\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{xlnx}}\right)\sim\frac{\mathrm{1}}{\mathrm{xlnx}}\:\Rightarrow\mathrm{xlnxln}\left(\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{ln}}\right)\sim\:\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{e} \\ $$
