Question Number 138383 by henderson last updated on 12/Apr/21
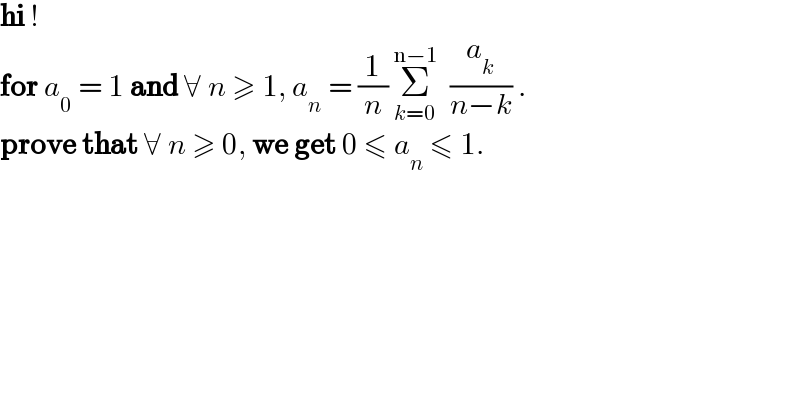
$$\boldsymbol{\mathrm{hi}}\:! \\ $$$$\boldsymbol{\mathrm{for}}\:{a}_{\mathrm{0}} \:=\:\mathrm{1}\:\boldsymbol{\mathrm{and}}\:\forall\:{n}\:\geqslant\:\mathrm{1},\:{a}_{{n}} \:=\:\frac{\mathrm{1}}{{n}}\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\:\:\frac{{a}_{{k}} }{{n}−{k}}\:. \\ $$$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\forall\:{n}\:\geqslant\:\mathrm{0},\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\mathrm{0}\:\leqslant\:{a}_{{n}} \:\leqslant\:\mathrm{1}. \\ $$
Commented by mitica last updated on 13/Apr/21
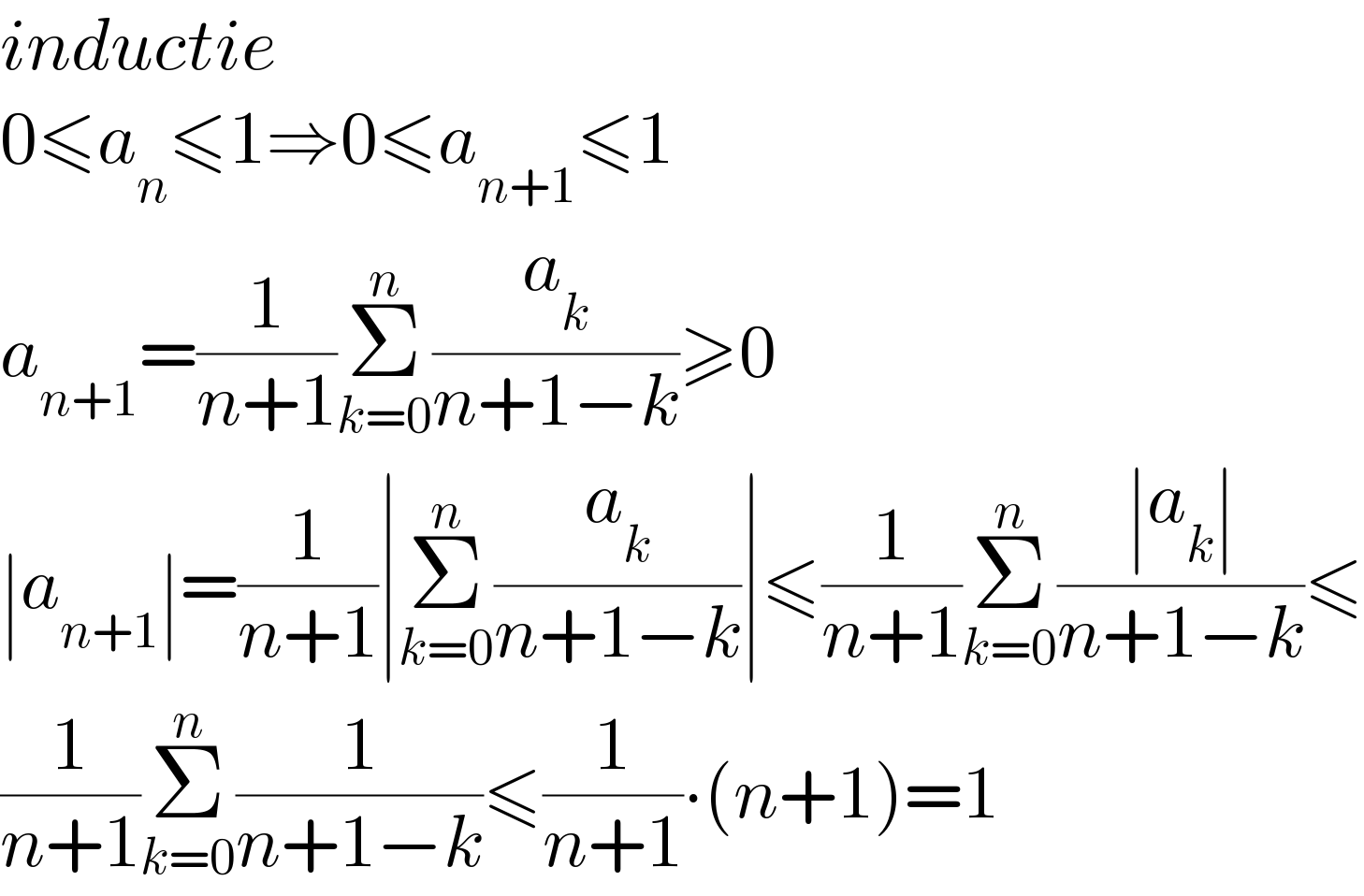
$${inductie} \\ $$$$\mathrm{0}\leqslant{a}_{{n}} \leqslant\mathrm{1}\Rightarrow\mathrm{0}\leqslant{a}_{{n}+\mathrm{1}} \leqslant\mathrm{1} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{{n}+\mathrm{1}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{a}_{{k}} }{{n}+\mathrm{1}−{k}}\geqslant\mathrm{0} \\ $$$$\mid{a}_{{n}+\mathrm{1}} \mid=\frac{\mathrm{1}}{{n}+\mathrm{1}}\mid\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{a}_{{k}} }{{n}+\mathrm{1}−{k}}\mid\leqslant\frac{\mathrm{1}}{{n}+\mathrm{1}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mid{a}_{{k}} \mid}{{n}+\mathrm{1}−{k}}\leqslant \\ $$$$\frac{\mathrm{1}}{{n}+\mathrm{1}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}−{k}}\leqslant\frac{\mathrm{1}}{{n}+\mathrm{1}}\centerdot\left({n}+\mathrm{1}\right)=\mathrm{1} \\ $$
Commented by henderson last updated on 13/Apr/21

$$\mathrm{thank}\:\mathrm{u},\:\mathrm{sir}\:\mathrm{mitica}\:! \\ $$
