Menu Close

homogenous-differential-equation-2xy-y-2-dr-2x-2-dy-0-y-e-x-e-

Tinku Tara 0 Comments
Pin




Question Number 67899 by ramirez105 last updated on 01/Sep/19
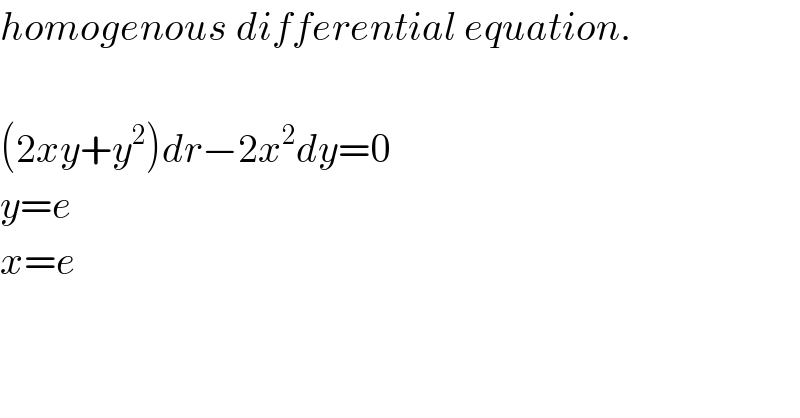
homogenous differential equation. (2xy+y^2 )dr−2x^2 dy=0 y=e x=e
$${homogenous}\:{differential}\:{equation}. \\ $$$$ \\ $$$$\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right){dr}−\mathrm{2}{x}^{\mathrm{2}} {dy}=\mathrm{0} \\ $$$${y}={e} \\ $$$${x}={e} \\ $$
Commented by AnJan_Math_Max last updated on 02/Sep/19
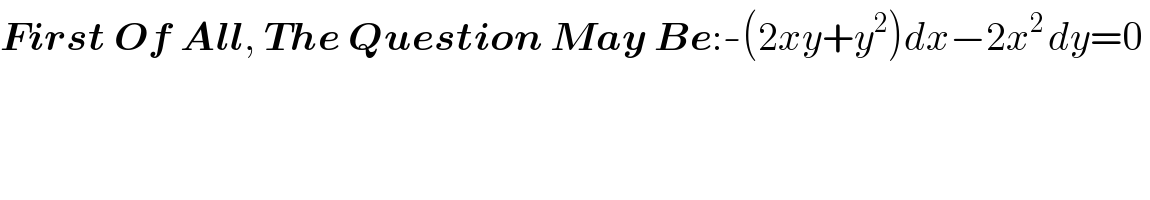
First Of All, The Question May Be:-(2xy+y^2 )dx−2x^(2 ) dy=0
$$\boldsymbol{{First}}\:\boldsymbol{{Of}}\:\boldsymbol{{All}},\:\boldsymbol{{The}}\:\boldsymbol{{Question}}\:\boldsymbol{{May}}\:\boldsymbol{{Be}}:-\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right){dx}−\mathrm{2}{x}^{\mathrm{2}\:} {dy}=\mathrm{0}\: \\ $$
Commented by mathmax by abdo last updated on 02/Sep/19
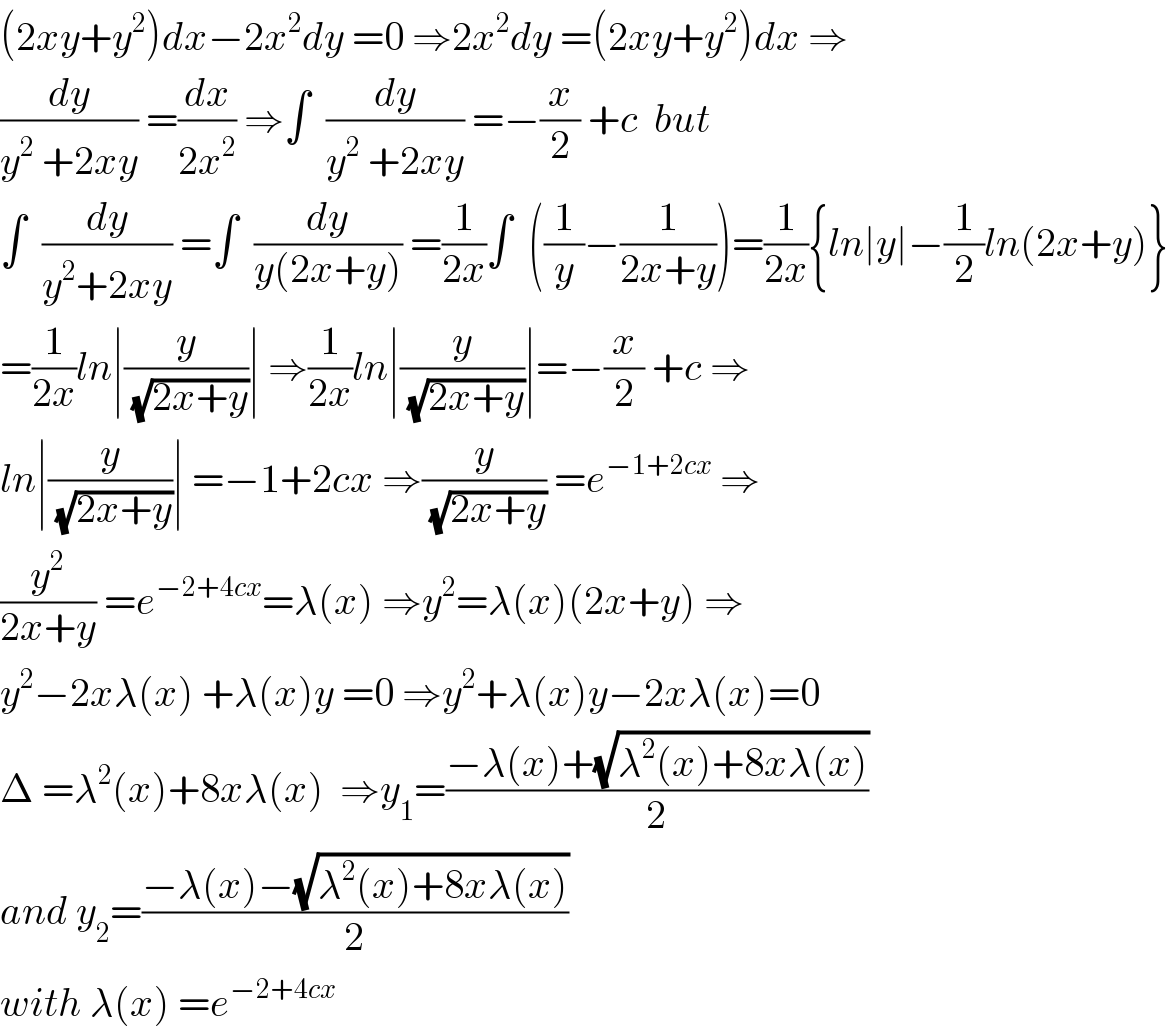
(2xy+y^2 )dx−2x^2 dy =0 ⇒2x^2 dy =(2xy+y^2 )dx ⇒ (dy/(y^2 +2xy)) =(dx/(2x^2 )) ⇒∫ (dy/(y^2 +2xy)) =−(x/2) +c but ∫ (dy/(y^2 +2xy)) =∫ (dy/(y(2x+y))) =(1/(2x))∫ ((1/y)−(1/(2x+y)))=(1/(2x)){ln∣y∣−(1/2)ln(2x+y)} =(1/(2x))ln∣(y/( (√(2x+y))))∣ ⇒(1/(2x))ln∣(y/( (√(2x+y))))∣=−(x/2) +c ⇒ ln∣(y/( (√(2x+y))))∣ =−1+2cx ⇒(y/( (√(2x+y)))) =e^(−1+2cx) ⇒ (y^2 /(2x+y)) =e^(−2+4cx) =λ(x) ⇒y^2 =λ(x)(2x+y) ⇒ y^2 −2xλ(x) +λ(x)y =0 ⇒y^2 +λ(x)y−2xλ(x)=0 Δ =λ^2 (x)+8xλ(x) ⇒y_1 =((−λ(x)+(√(λ^2 (x)+8xλ(x))))/2) and y_2 =((−λ(x)−(√(λ^2 (x)+8xλ(x))))/2) with λ(x) =e^(−2+4cx)
$$\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right){dx}−\mathrm{2}{x}^{\mathrm{2}} {dy}\:=\mathrm{0}\:\Rightarrow\mathrm{2}{x}^{\mathrm{2}} {dy}\:=\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right){dx}\:\Rightarrow \\ $$$$\frac{{dy}}{{y}^{\mathrm{2}} \:+\mathrm{2}{xy}}\:=\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} }\:\Rightarrow\int\:\:\frac{{dy}}{{y}^{\mathrm{2}} \:+\mathrm{2}{xy}}\:=−\frac{{x}}{\mathrm{2}}\:+{c}\:\:{but} \\ $$$$\int\:\:\frac{{dy}}{{y}^{\mathrm{2}} +\mathrm{2}{xy}}\:=\int\:\:\frac{{dy}}{{y}\left(\mathrm{2}{x}+{y}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}{x}}\int\:\:\left(\frac{\mathrm{1}}{{y}}−\frac{\mathrm{1}}{\mathrm{2}{x}+{y}}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{{ln}\mid{y}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{x}+{y}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{x}}{ln}\mid\frac{{y}}{\:\sqrt{\mathrm{2}{x}+{y}}}\mid\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{x}}{ln}\mid\frac{{y}}{\:\sqrt{\mathrm{2}{x}+{y}}}\mid=−\frac{{x}}{\mathrm{2}}\:+{c}\:\Rightarrow \\ $$$${ln}\mid\frac{{y}}{\:\sqrt{\mathrm{2}{x}+{y}}}\mid\:=−\mathrm{1}+\mathrm{2}{cx}\:\Rightarrow\frac{{y}}{\:\sqrt{\mathrm{2}{x}+{y}}}\:={e}^{−\mathrm{1}+\mathrm{2}{cx}} \:\Rightarrow \\ $$$$\frac{{y}^{\mathrm{2}} }{\mathrm{2}{x}+{y}}\:={e}^{−\mathrm{2}+\mathrm{4}{cx}} =\lambda\left({x}\right)\:\Rightarrow{y}^{\mathrm{2}} =\lambda\left({x}\right)\left(\mathrm{2}{x}+{y}\right)\:\Rightarrow \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{x}\lambda\left({x}\right)\:+\lambda\left({x}\right){y}\:=\mathrm{0}\:\Rightarrow{y}^{\mathrm{2}} +\lambda\left({x}\right){y}−\mathrm{2}{x}\lambda\left({x}\right)=\mathrm{0} \\ $$$$\Delta\:=\lambda^{\mathrm{2}} \left({x}\right)+\mathrm{8}{x}\lambda\left({x}\right)\:\:\Rightarrow{y}_{\mathrm{1}} =\frac{−\lambda\left({x}\right)+\sqrt{\lambda^{\mathrm{2}} \left({x}\right)+\mathrm{8}{x}\lambda\left({x}\right)}}{\mathrm{2}} \\ $$$${and}\:{y}_{\mathrm{2}} =\frac{−\lambda\left({x}\right)−\sqrt{\lambda^{\mathrm{2}} \left({x}\right)+\mathrm{8}{x}\lambda\left({x}\right)}}{\mathrm{2}} \\ $$$${with}\:\lambda\left({x}\right)\:={e}^{−\mathrm{2}+\mathrm{4}{cx}} \\ $$
Answered by AnJan_Math_Max last updated on 02/Sep/19
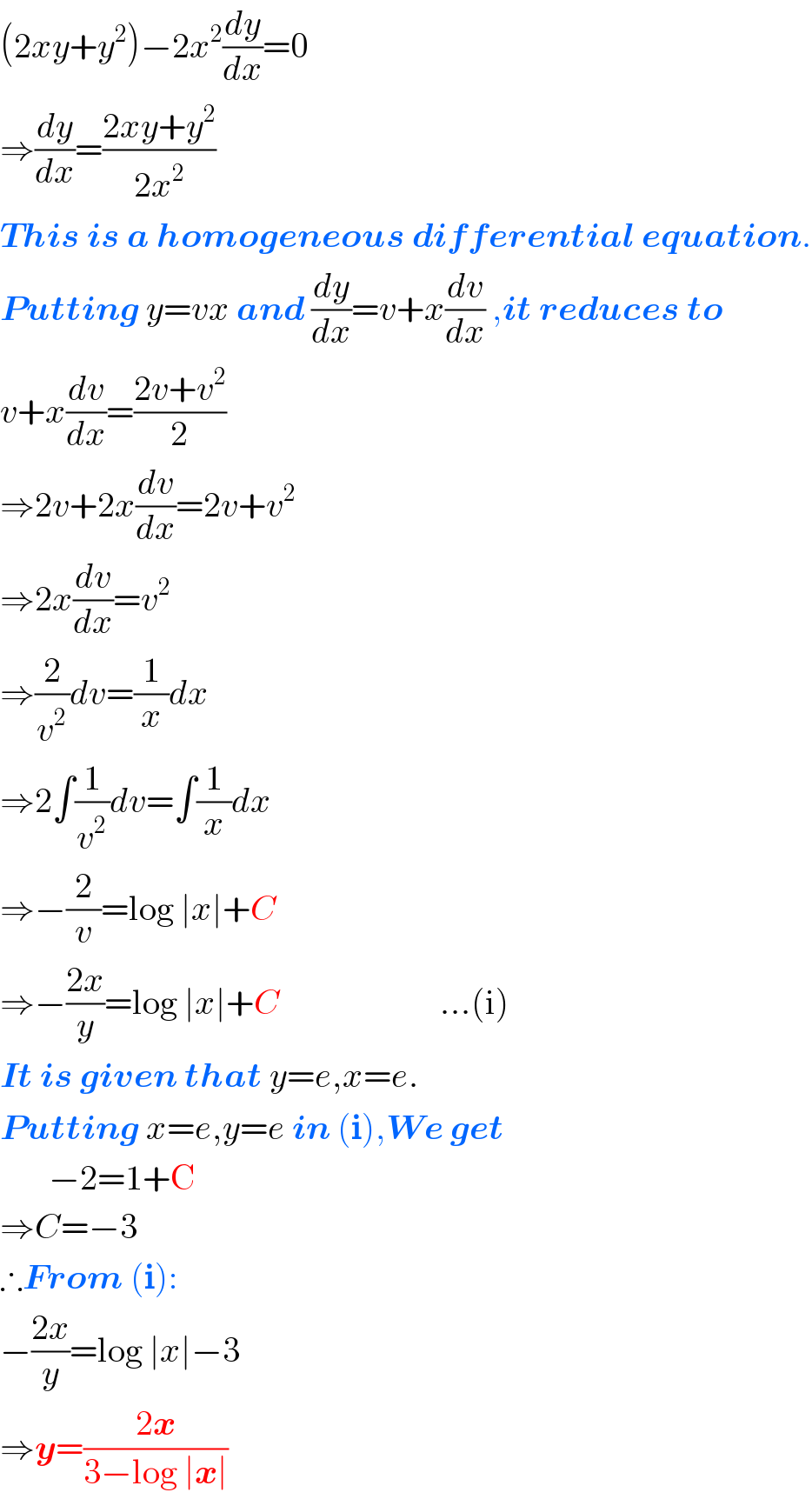
(2xy+y^2 )−2x^2 (dy/dx)=0 ⇒(dy/dx)=((2xy+y^2 )/(2x^2 )) This is a homogeneous differential equation. Putting y=vx and (dy/dx)=v+x(dv/dx) ,it reduces to v+x(dv/dx)=((2v+v^2 )/2) ⇒2v+2x(dv/dx)=2v+v^2 ⇒2x(dv/dx)=v^2 ⇒(2/v^2 )dv=(1/x)dx ⇒2∫(1/v^2 )dv=∫(1/x)dx ⇒−(2/v)=log ∣x∣+C ⇒−((2x)/y)=log ∣x∣+C ...(i) It is given that y=e,x=e. Putting x=e,y=e in (i),We get −2=1+C ⇒C=−3 ∴From (i): −((2x)/y)=log ∣x∣−3 ⇒y=((2x)/(3−log ∣x∣))
$$\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right)−\mathrm{2}{x}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{2}{xy}+{y}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\boldsymbol{{This}}\:\boldsymbol{{is}}\:\boldsymbol{{a}}\:\boldsymbol{{homogeneous}}\:\boldsymbol{{differential}}\:\boldsymbol{{equation}}. \\ $$$$\boldsymbol{{Putting}}\:{y}={vx}\:\boldsymbol{{and}}\:\frac{{dy}}{{dx}}={v}+{x}\frac{{dv}}{{dx}}\:,\boldsymbol{{it}}\:\boldsymbol{{reduces}}\:\boldsymbol{{to}} \\ $$$${v}+{x}\frac{{dv}}{{dx}}=\frac{\mathrm{2}{v}+{v}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{v}+\mathrm{2}{x}\frac{{dv}}{{dx}}=\mathrm{2}{v}+{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{x}\frac{{dv}}{{dx}}={v}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}}{{v}^{\mathrm{2}} }{dv}=\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\Rightarrow\mathrm{2}\int\frac{\mathrm{1}}{{v}^{\mathrm{2}} }{dv}=\int\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\Rightarrow−\frac{\mathrm{2}}{{v}}=\mathrm{log}\:\mid{x}\mid+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow−\frac{\mathrm{2}{x}}{{y}}=\mathrm{log}\:\mid{x}\mid+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$\boldsymbol{{It}}\:\boldsymbol{{is}}\:\boldsymbol{{given}}\:\boldsymbol{{that}}\:{y}={e},{x}={e}. \\ $$$$\boldsymbol{{Putting}}\:{x}={e},{y}={e}\:\boldsymbol{{in}}\:\left(\boldsymbol{\mathrm{i}}\right),\boldsymbol{{We}}\:\boldsymbol{{get}} \\ $$$$\:\:\:\:\:\:\:−\mathrm{2}=\mathrm{1}+\mathrm{C} \\ $$$$\Rightarrow{C}=−\mathrm{3} \\ $$$$\therefore\boldsymbol{{From}}\:\left(\boldsymbol{\mathrm{i}}\right): \\ $$$$−\frac{\mathrm{2}{x}}{{y}}=\mathrm{log}\:\mid{x}\mid−\mathrm{3} \\ $$$$\Rightarrow\boldsymbol{{y}}=\frac{\mathrm{2}\boldsymbol{{x}}}{\mathrm{3}−\mathrm{log}\:\mid\boldsymbol{{x}}\mid} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *