Question Number 10114 by JAZAR last updated on 24/Jan/17
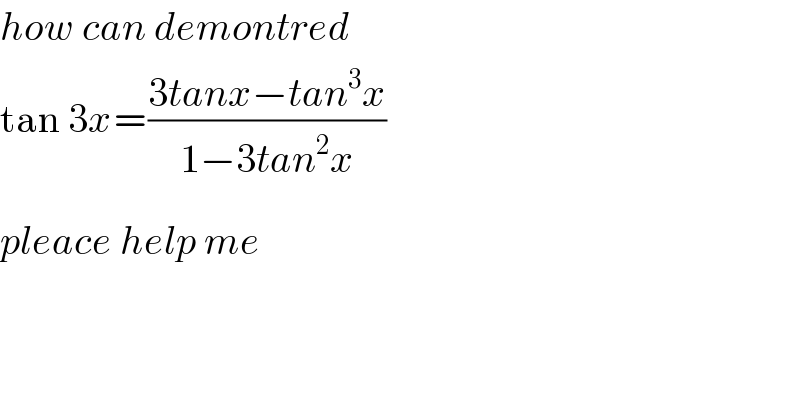
$${how}\:{can}\:{demontred} \\ $$$$\mathrm{tan}\:\mathrm{3}{x}\underset{\:\:\:\:\:\:\:\:\:} {=}\frac{\mathrm{3}{tanx}−{tan}^{\mathrm{3}} {x}}{\underset{} {\mathrm{1}}−\mathrm{3}{tan}^{\mathrm{2}} {x}} \\ $$$${pleace}\:{help}\:{me} \\ $$
Answered by mrW1 last updated on 24/Jan/17
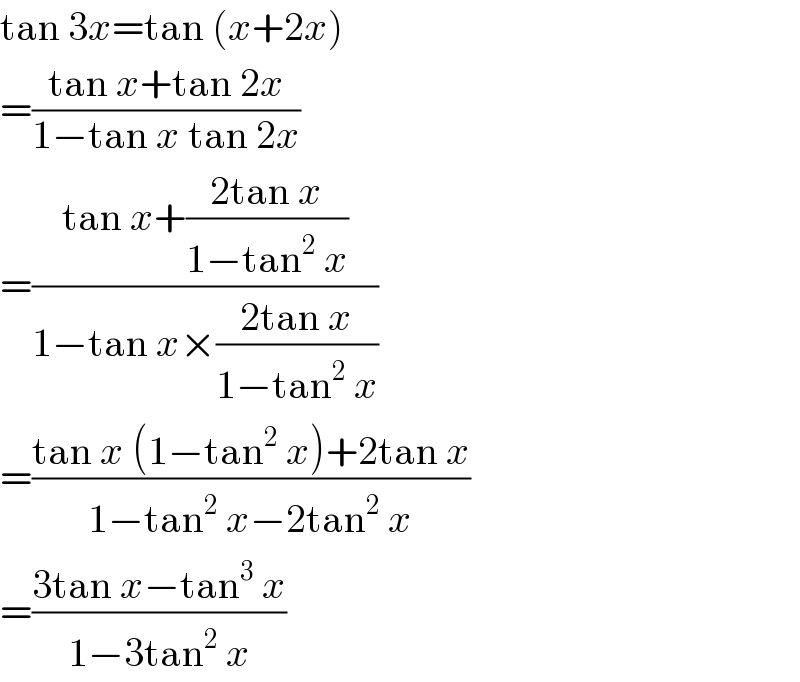
$$\mathrm{tan}\:\mathrm{3}{x}=\mathrm{tan}\:\left({x}+\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{1}−\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{tan}\:{x}+\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}}{\mathrm{1}−\mathrm{tan}\:{x}×\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}} \\ $$$$=\frac{\mathrm{tan}\:{x}\:\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}\right)+\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}−\mathrm{2tan}^{\mathrm{2}} \:{x}}\: \\ $$$$=\frac{\mathrm{3tan}\:{x}−\mathrm{tan}^{\mathrm{3}} \:{x}}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \:{x}} \\ $$
