how-do-we-calculate-k-0-n-k2-k-

Question Number 134200 by Abdoulaye last updated on 28/Feb/21

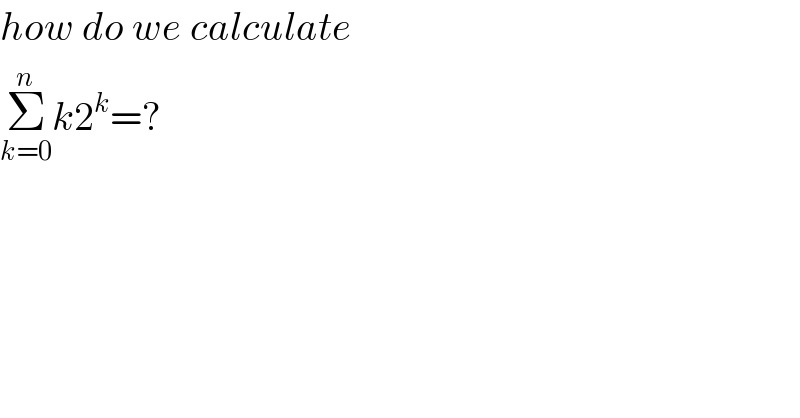
$${how}\:{do}\:{we}\:{calculate} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} =? \\ $$

Answered by mr W last updated on 01/Mar/21

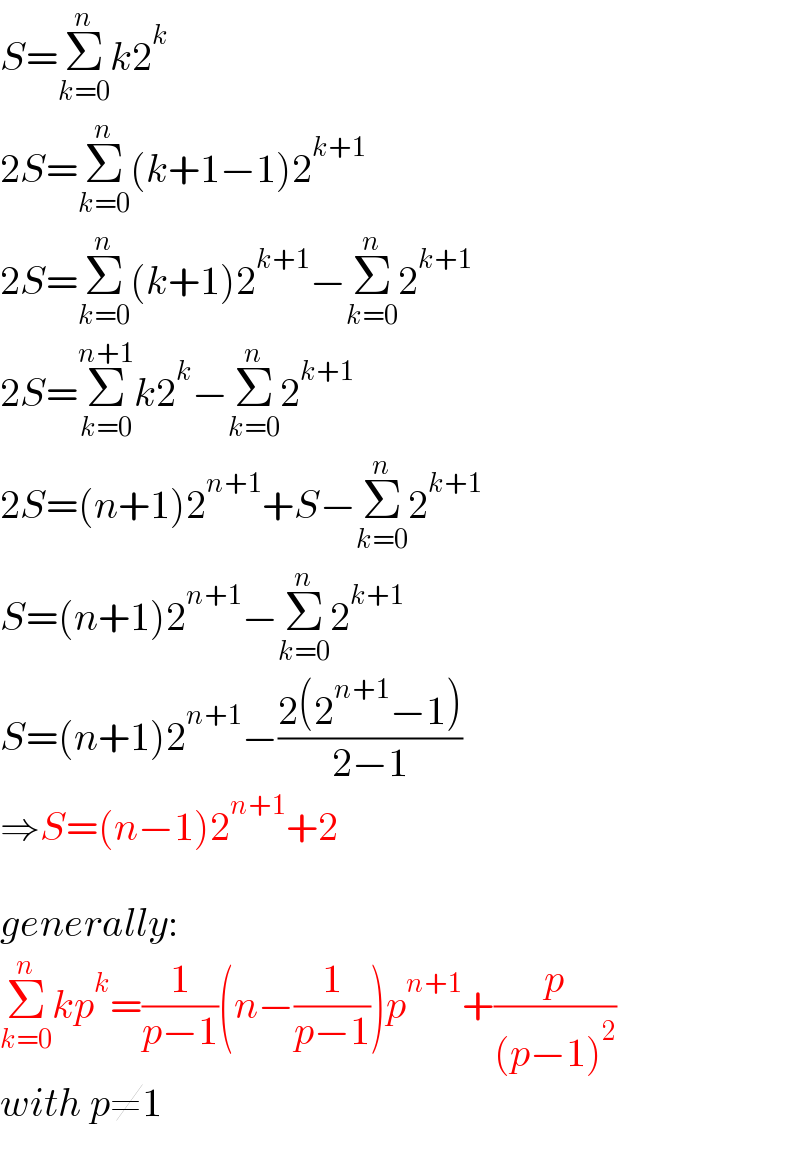
S=Σ_(k=0) ^n k2^k 2S=Σ_(k=0) ^n (k+1−1)2^(k+1) 2S=Σ_(k=0) ^n (k+1)2^(k+1) −Σ_(k=0) ^n 2^(k+1) 2S=Σ_(k=0) ^(n+1) k2^k −Σ_(k=0) ^n 2^(k+1) 2S=(n+1)2^(n+1) +S−Σ_(k=0) ^n 2^(k+1) S=(n+1)2^(n+1) −Σ_(k=0) ^n 2^(k+1) S=(n+1)2^(n+1) −((2(2^(n+1) −1))/(2−1)) ⇒S=(n−1)2^(n+1) +2 generally: Σ_(k=0) ^n kp^k =(1/(p−1))(n−(1/(p−1)))p^(n+1) +(p/((p−1)^2 )) with p≠1

$${S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}−\mathrm{1}\right)\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{2}^{{k}+\mathrm{1}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\mathrm{2}{S}=\underset{{k}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}{k}\mathrm{2}^{{k}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\mathrm{2}{S}=\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +{S}−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$${S}=\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}+\mathrm{1}} \\ $$$${S}=\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} −\frac{\mathrm{2}\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}} \\ $$$$\Rightarrow{S}=\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$$$ \\ $$$${generally}: \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}} =\frac{\mathrm{1}}{{p}−\mathrm{1}}\left({n}−\frac{\mathrm{1}}{{p}−\mathrm{1}}\right){p}^{{n}+\mathrm{1}} +\frac{{p}}{\left({p}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${with}\:{p}\neq\mathrm{1} \\ $$

Commented by Abdoulaye last updated on 01/Mar/21

$${thank}\:{you}\:{sir} \\ $$

Answered by Ñï= last updated on 01/Mar/21

Σ_(k=0) ^n k2^k =[xDΣ_(k=0) ^n x^k ]_(x=2) =xD[((x^(n+1) −1)/(x−1))]_(x=2) =((nx^(n+2) −(n+1)x^(n+1) +x)/((x−1)^2 ))∣_(x=2) =n2^(n+2) −(n+1)2^(n+1) +2 =(n−1)2^(n+1) +2

$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\mathrm{2}^{{k}} \\ $$$$=\left[{xD}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{k}} \right]_{{x}=\mathrm{2}} \\ $$$$={xD}\left[\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right]_{{x}=\mathrm{2}} \\ $$$$=\frac{{nx}^{{n}+\mathrm{2}} −\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\mid_{{x}=\mathrm{2}} \\ $$$$={n}\mathrm{2}^{{n}+\mathrm{2}} −\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$$$=\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{2} \\ $$

Facebook Tweet Pin

how-do-we-calculate-k-0-n-k2-k-

Leave a Reply Cancel reply