How-do-you-find-the-interval-in-which-x-belongs-such-that-sinx-cosx-sinx-cosx-

Question Number 134538 by bemath last updated on 05/Mar/21

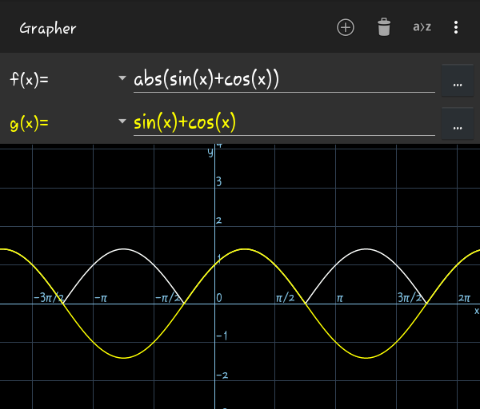
$$ \\ $$How do you find the interval in which x belongs such that |sinx+cosx|=sinx + cosx?

Answered by EDWIN88 last updated on 05/Mar/21

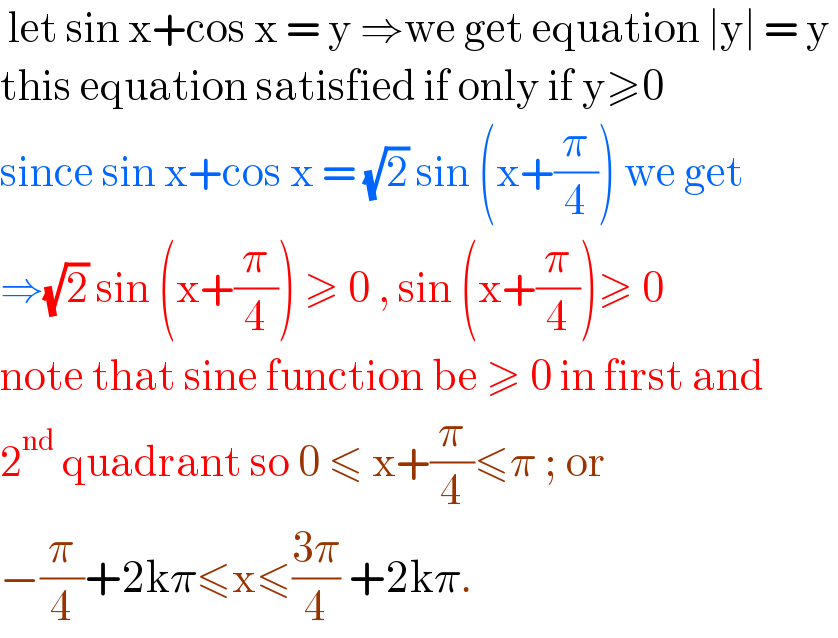
let sin x+cos x = y ⇒we get equation ∣y∣ = y this equation satisfied if only if y≥0 since sin x+cos x = (√2) sin (x+(π/4)) we get ⇒(√2) sin (x+(π/4)) ≥ 0 , sin (x+(π/4))≥ 0 note that sine function be ≥ 0 in first and 2^(nd) quadrant so 0 ≤ x+(π/4)≤π ; or −(π/4)+2kπ≤x≤((3π)/4) +2kπ.

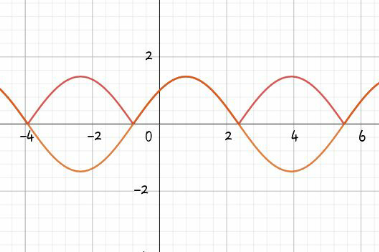
$$\:\mathrm{let}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{y}\:\Rightarrow\mathrm{we}\:\mathrm{get}\:\mathrm{equation}\:\mid\mathrm{y}\mid\:=\:\mathrm{y}\: \\ $$$$\mathrm{this}\:\mathrm{equation}\:\mathrm{satisfied}\:\mathrm{if}\:\mathrm{only}\:\mathrm{if}\:\mathrm{y}\geqslant\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\:\geqslant\:\mathrm{0}\:,\:\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\geqslant\:\mathrm{0} \\ $$$$\mathrm{note}\:\mathrm{that}\:\mathrm{sine}\:\mathrm{function}\:\mathrm{be}\:\geqslant\:\mathrm{0}\:\mathrm{in}\:\mathrm{first}\:\mathrm{and}\: \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{quadrant}\:\mathrm{so}\:\mathrm{0}\:\leqslant\:\mathrm{x}+\frac{\pi}{\mathrm{4}}\leqslant\pi\:;\:\mathrm{or}\: \\ $$$$−\frac{\pi}{\mathrm{4}}+\mathrm{2k}\pi\leqslant\mathrm{x}\leqslant\frac{\mathrm{3}\pi}{\mathrm{4}}\:+\mathrm{2k}\pi. \\ $$

Commented by EDWIN88 last updated on 05/Mar/21