Menu Close

How-do-you-solve-for-2cos-3-x-sinx-3sin-2-x-cos-x-0-

Tinku Tara 0 Comments
Pin




Question Number 135974 by liberty last updated on 17/Mar/21
How do you solve for 2cos^3(x) + sinx - 3sin^2 (x) cos(x) =0?
$$ \\ $$How do you solve for 2cos^3(x) + sinx – 3sin^2 (x) cos(x) =0?
Commented by mr W last updated on 17/Mar/21
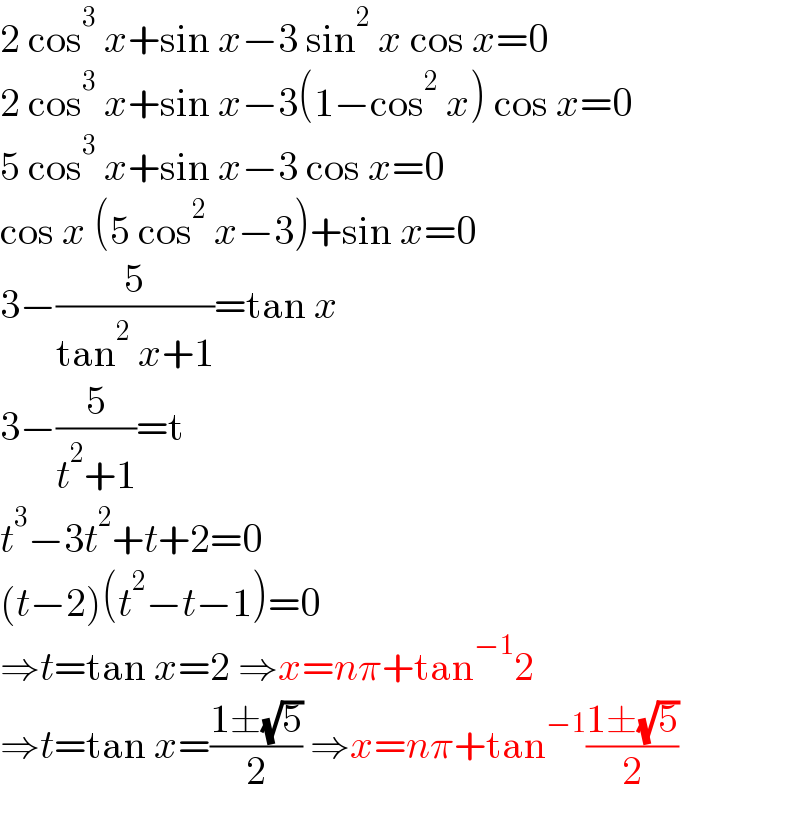
2 cos^3 x+sin x−3 sin^2 x cos x=0 2 cos^3 x+sin x−3(1−cos^2 x) cos x=0 5 cos^3 x+sin x−3 cos x=0 cos x (5 cos^2 x−3)+sin x=0 3−(5/(tan^2 x+1))=tan x 3−(5/(t^2 +1))=t t^3 −3t^2 +t+2=0 (t−2)(t^2 −t−1)=0 ⇒t=tan x=2 ⇒x=nπ+tan^(−1) 2 ⇒t=tan x=((1±(√5))/2) ⇒x=nπ+tan^(−1) ((1±(√5))/2)
$$\mathrm{2}\:\mathrm{cos}^{\mathrm{3}} \:{x}+\mathrm{sin}\:{x}−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\mathrm{2}\:\mathrm{cos}^{\mathrm{3}} \:{x}+\mathrm{sin}\:{x}−\mathrm{3}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}\right)\:\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\mathrm{5}\:\mathrm{cos}^{\mathrm{3}} \:{x}+\mathrm{sin}\:{x}−\mathrm{3}\:\mathrm{cos}\:{x}=\mathrm{0} \\ $$$$\mathrm{cos}\:{x}\:\left(\mathrm{5}\:\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{3}\right)+\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\mathrm{3}−\frac{\mathrm{5}}{\mathrm{tan}^{\mathrm{2}} \:{x}+\mathrm{1}}=\mathrm{tan}\:{x} \\ $$$$\mathrm{3}−\frac{\mathrm{5}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{t} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +{t}+\mathrm{2}=\mathrm{0} \\ $$$$\left({t}−\mathrm{2}\right)\left({t}^{\mathrm{2}} −{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:{x}=\mathrm{2}\:\Rightarrow{x}={n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{2} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\:\Rightarrow{x}={n}\pi+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by liberty last updated on 17/Mar/21
replacing sin x=sin^3 x+sin x cos^2 x (•) 2cos^3 x+sin^3 x+sin xcos^2 x−3sin^2 x cos x = 0 divided by cos^3 x 2+tan^3 x+tan x−3tan^2 x = 0 ⇒tan^3 x−3tan^2 x+tan x+2 = 0 let tan x = u ⇒u^3 −3u^2 +u+2 = 0 (u−2)(u^2 −u−1)=0 → { ((u=2⇒tan x=2)),((u = ((1±(√5))/2)⇒tan x=((1±(√5))/2))) :}
$${replacing}\:\mathrm{sin}\:{x}=\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{sin}\:{x}\:\mathrm{cos}\:^{\mathrm{2}} {x} \\ $$$$\left(\bullet\right)\:\mathrm{2cos}\:^{\mathrm{3}} {x}+\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{sin}\:{x}\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{3sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:{x}\:=\:\mathrm{0} \\ $$$${divided}\:{by}\:\mathrm{cos}\:^{\mathrm{3}} {x} \\ $$$$\mathrm{2}+\mathrm{tan}\:^{\mathrm{3}} {x}+\mathrm{tan}\:{x}−\mathrm{3tan}\:^{\mathrm{2}} {x}\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\mathrm{tan}\:^{\mathrm{3}} {x}−\mathrm{3tan}\:^{\mathrm{2}} {x}+\mathrm{tan}\:{x}+\mathrm{2}\:=\:\mathrm{0} \\ $$$${let}\:\mathrm{tan}\:{x}\:=\:{u} \\ $$$$\Rightarrow{u}^{\mathrm{3}} −\mathrm{3}{u}^{\mathrm{2}} +{u}+\mathrm{2}\:=\:\mathrm{0} \\ $$$$\left({u}−\mathrm{2}\right)\left({u}^{\mathrm{2}} −{u}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\rightarrow\begin{cases}{{u}=\mathrm{2}\Rightarrow\mathrm{tan}\:{x}=\mathrm{2}}\\{{u}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\mathrm{tan}\:{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}}\end{cases} \\ $$
Answered by MJS_new last updated on 17/Mar/21
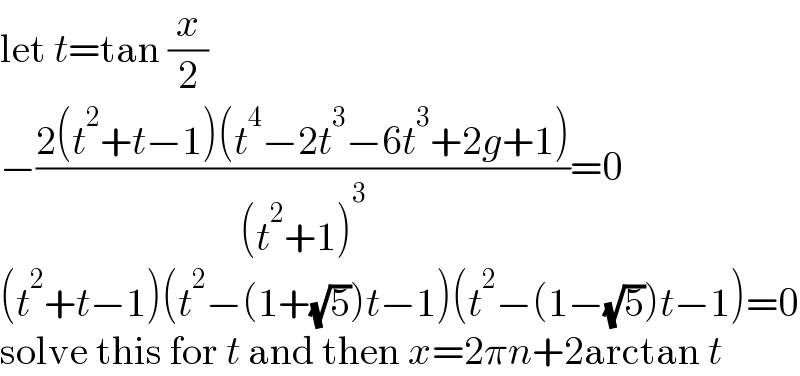
let t=tan (x/2) −((2(t^2 +t−1)(t^4 −2t^3 −6t^3 +2g+1))/((t^2 +1)^3 ))=0 (t^2 +t−1)(t^2 −(1+(√5))t−1)(t^2 −(1−(√5))t−1)=0 solve this for t and then x=2πn+2arctan t
$$\mathrm{let}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$−\frac{\mathrm{2}\left({t}^{\mathrm{2}} +{t}−\mathrm{1}\right)\left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{6}{t}^{\mathrm{3}} +\mathrm{2}{g}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{t}\:\mathrm{and}\:\mathrm{then}\:{x}=\mathrm{2}\pi{n}+\mathrm{2arctan}\:{t} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *