Question Number 3172 by Rasheed Soomro last updated on 07/Dec/15

$$\mathcal{H}{ow}\:{many}\:{different}\:\:{clock}−{type}\:{dials}\:{can}\:{be}\:{made}\: \\ $$$${containing}\:{first}\:{n}\:{natual}\:{numbers}\:{with}\:{the}\:{property} \\ $$$${that}\:{sum}\:{of}\:\:{any}\:{two}\:{numbers}\:{of}\:{consecutive}\:{positions}\:{be} \\ $$$${a}\:{prime}\:{number}. \\ $$$$\mathbb{N}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},…\right\} \\ $$
Commented by Rasheed Soomro last updated on 07/Dec/15

$$\mathcal{F}{or}\:{n}=\mathrm{1}\:{there}\:{is}\:{no}\:{such}\:{dial}. \\ $$$$\mathcal{F}{or}\:{n}=\mathrm{2}\:{there}\:{is}\:\mathrm{1}\:{such}\:{dial}.\:\: \\ $$$$\mathcal{F}{or}\:{n}=\mathrm{3}\:{there}\:{is}\:{no}\:{such}\:{dial}. \\ $$$$\mathcal{F}{or}\:{n}=\mathrm{4}\:{there}\:{are}\:{two}\:{such}\:{dials}:\:\mathrm{12341},\mathrm{14321}\: \\ $$$$\mathcal{F}{or}\:{n}=\mathrm{5}\::\:\:\: \\ $$$$\vdots \\ $$$$\mathcal{F}{or}\:{n}\:{there}\:{are}\:{m}\:{such}\:{dials}.\:\:\:\mathcal{W}{hat}\:{is}\:{m}? \\ $$
Answered by prakash jain last updated on 06/Dec/15

$$\mathrm{No}\:\mathrm{such}\:\mathrm{formula}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that} \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{prime}\:\mathrm{numbers}. \\ $$
Commented by Rasheed Soomro last updated on 07/Dec/15
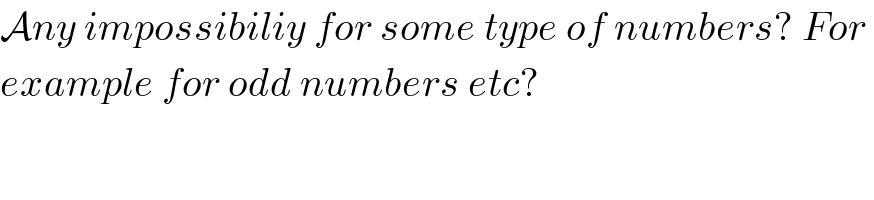
$$\mathcal{A}{ny}\:{impossibiliy}\:{for}\:{some}\:{type}\:{of}\:{numbers}?\:{For}\: \\ $$$${example}\:{for}\:{odd}\:{numbers}\:{etc}? \\ $$
