How-many-dimention-s-does-the-point-have-

Question Number 3850 by Rasheed Soomro last updated on 22/Dec/15

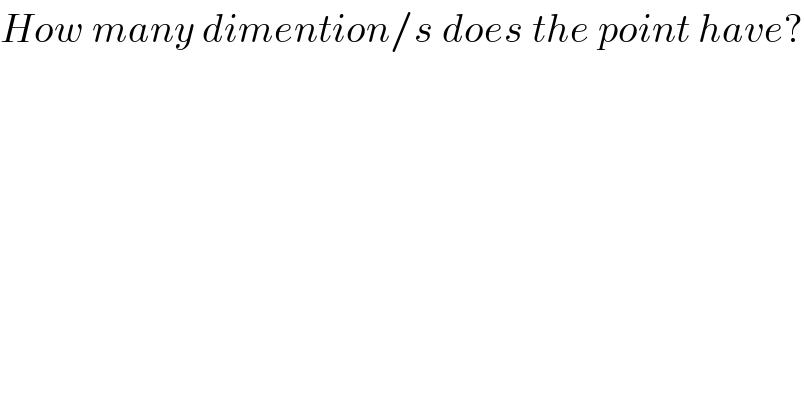
H o w m a n y d i m e n t i o n / s d o e s t h e p o i n t h a v e ?

Commented by prakash jain last updated on 22/Dec/15

In 3 D cartesian coordinate you need (x, y, z)

to uniquely describe a point .

Commented by Rasheed Soomro last updated on 22/Dec/15

In 2 D (x, y) is needed to describe apoint .

Does this mean that a point can be considered

of any dimention / s ?

Commented by 123456 last updated on 22/Dec/15

0

Commented by prakash jain last updated on 22/Dec/15

A point itself is dimensionless (L^{0}) .

Positioning of point or line or any figure

in n - dimension space requires information

about all dimensions .

Commented by Rasheed Soomro last updated on 22/Dec/15

I s^{'} t h e p o i n t h a s n o d i m e n t i o n^{'} i s

a postulate a b o u t p o i n t ?

[0, 1] i s a n o l o g u s t o l i n e s e g m e n t

(- \infty, + \infty) i s a n o l o g u s t o l i n e, I t h i n k .

Commented by 123456 last updated on 22/Dec/15

a line is made by inifnite number of points

example :

suppose that each number is a point, then

look at

[0, 1]

its a line, and you can choose infinite

numbers from these line

Commented by Filup last updated on 23/Dec/15

A point is dimensionless but it points

in all directions

Facebook Tweet Pin