Question Number 76495 by mathocean1 last updated on 27/Dec/19
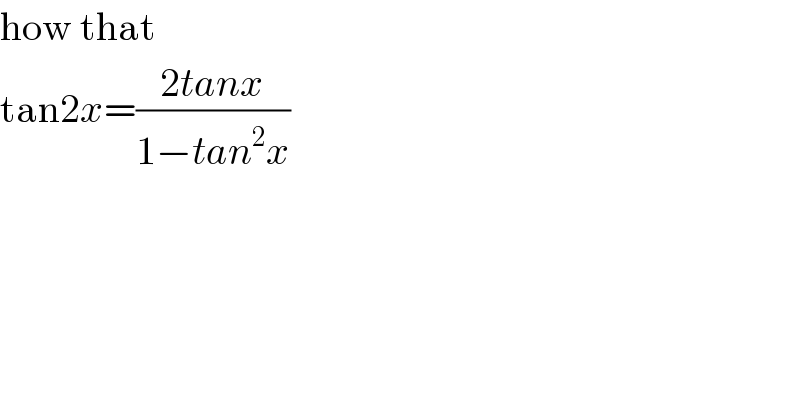
$$\mathrm{how}\:\mathrm{that} \\ $$$$\mathrm{tan2}{x}=\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$
Commented by mathmax by abdo last updated on 27/Dec/19

$${due}\:{to}\:{formula}\:\:{tan}\left(\mathrm{2}{x}\right)={tan}\left({x}+{x}\right)\:=\frac{{tanx}+{tanx}}{\mathrm{1}−{tanx}.{tanx}} \\ $$$$=\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$
Commented by mathocean1 last updated on 27/Dec/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 27/Dec/19
$${you}\:{are}\:{welcome}. \\ $$
Commented by Kunal12588 last updated on 28/Dec/19
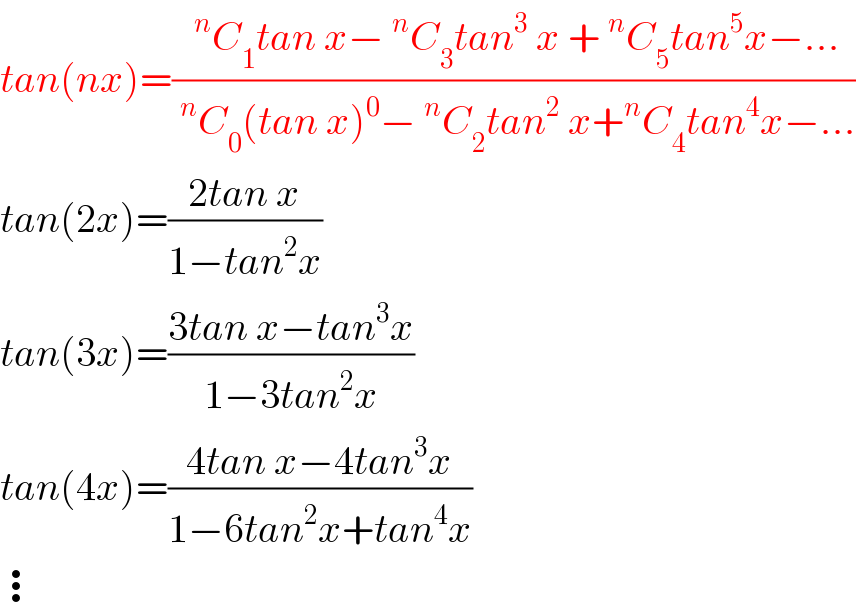
$${tan}\left({nx}\right)=\frac{\:^{{n}} {C}_{\mathrm{1}} {tan}\:{x}−\:^{{n}} {C}_{\mathrm{3}} {tan}^{\mathrm{3}} \:{x}\:+\:^{{n}} {C}_{\mathrm{5}} {tan}^{\mathrm{5}} {x}−…}{\:^{{n}} {C}_{\mathrm{0}} \left({tan}\:{x}\right)^{\mathrm{0}} −\:^{{n}} {C}_{\mathrm{2}} {tan}^{\mathrm{2}} \:{x}+^{{n}} {C}_{\mathrm{4}} {tan}^{\mathrm{4}} {x}−…} \\ $$$${tan}\left(\mathrm{2}{x}\right)=\frac{\mathrm{2}{tan}\:{x}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$${tan}\left(\mathrm{3}{x}\right)=\frac{\mathrm{3}{tan}\:{x}−{tan}^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} {x}} \\ $$$${tan}\left(\mathrm{4}{x}\right)=\frac{\mathrm{4}{tan}\:{x}−\mathrm{4}{tan}^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{6}{tan}^{\mathrm{2}} {x}+{tan}^{\mathrm{4}} {x}} \\ $$$$\vdots \\ $$
Commented by john santu last updated on 28/Dec/19
$${wawww}\:\:\:\:{great}\:{sir}\:{short}\:{cut}. \\ $$
Answered by $@ty@m123 last updated on 28/Dec/19

$${Alternative}\:{proof}: \\ $$$$\mathrm{tan}\:\mathrm{2}{x}=\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{2sin}\:{x}\mathrm{cos}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$$$=\frac{\left(\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\right)\boldsymbol{\div}\mathrm{cos}\:^{\mathrm{2}} {x}}{\left(\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)\boldsymbol{\div}\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}} \\ $$
