Question Number 137324 by greg_ed last updated on 01/Apr/21
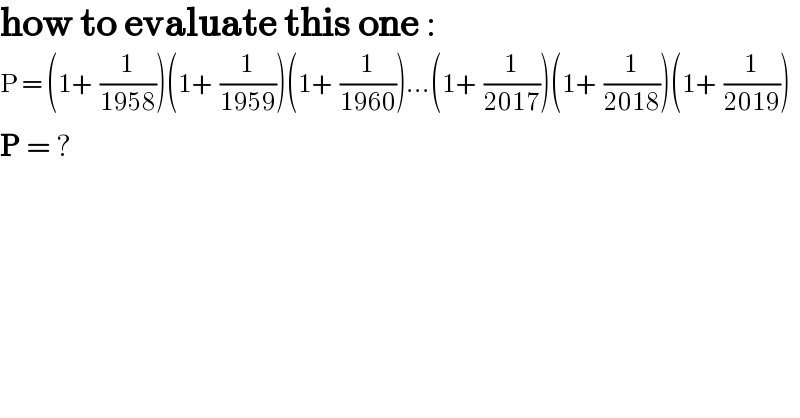
$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{evaluate}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{one}}\:: \\ $$$$\mathrm{P}\:=\:\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{1958}}\right)\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{1959}}\right)\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{1960}}\right)…\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2017}}\right)\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2018}}\right)\left(\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2019}}\right) \\ $$$$\boldsymbol{\mathrm{P}}\:=\:?\: \\ $$
Answered by som(math1967) last updated on 01/Apr/21
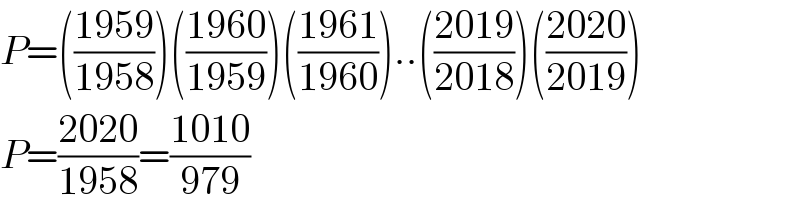
$${P}=\left(\frac{\mathrm{1959}}{\mathrm{1958}}\right)\left(\frac{\mathrm{1960}}{\mathrm{1959}}\right)\left(\frac{\mathrm{1961}}{\mathrm{1960}}\right)..\left(\frac{\mathrm{2019}}{\mathrm{2018}}\right)\left(\frac{\mathrm{2020}}{\mathrm{2019}}\right) \\ $$$${P}=\frac{\mathrm{2020}}{\mathrm{1958}}=\frac{\mathrm{1010}}{\mathrm{979}} \\ $$
Commented by greg_ed last updated on 01/Apr/21

$$\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{u}}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{much}},\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{som}}\left(\boldsymbol{\mathrm{math}}\mathrm{1967}\right) \\ $$
Commented by som(math1967) last updated on 01/Apr/21

$${welcome} \\ $$
