Question Number 136643 by Ñï= last updated on 24/Mar/21
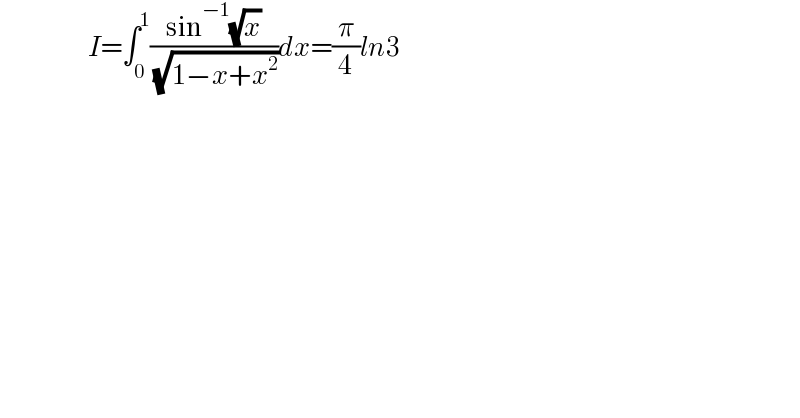
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{3} \\ $$
Answered by Ñï= last updated on 24/Mar/21
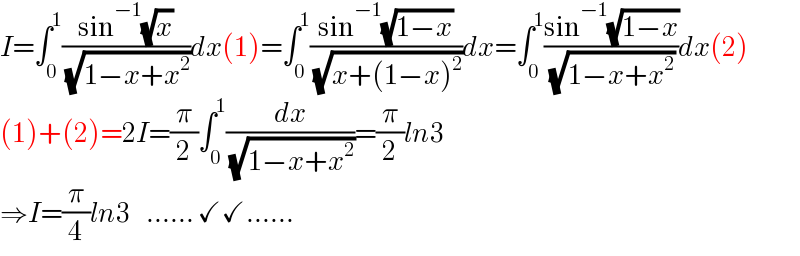
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \sqrt{\mathrm{1}−{x}}}{\:\sqrt{{x}+\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}^{−\mathrm{1}} \sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}{dx}\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)=\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}=\frac{\pi}{\mathrm{2}}{ln}\mathrm{3} \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{3}\:\:\:\:……\:\checkmark\checkmark…… \\ $$
Commented by mnjuly1970 last updated on 24/Mar/21
$$\:\:\:\:{very}\:{nice}\:{thanks}\:{alot}… \\ $$
