Question Number 139555 by snipers237 last updated on 28/Apr/21
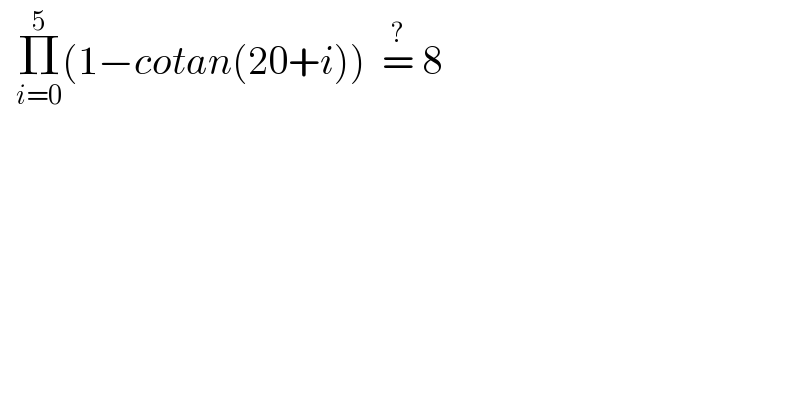
$$\:\:\underset{{i}=\mathrm{0}} {\overset{\mathrm{5}} {\prod}}\left(\mathrm{1}−{cotan}\left(\mathrm{20}+{i}\right)\right)\:\:\overset{?} {=}\:\mathrm{8} \\ $$
Answered by mr W last updated on 28/Apr/21

$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{25}°}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{25}°}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{1}−\frac{\mathrm{tan}\:\mathrm{20}°+\mathrm{tan}\:\mathrm{25}°}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{1}−\frac{\mathrm{tan}\:\mathrm{20}°+\mathrm{tan}\:\mathrm{25}°}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}×\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}{\mathrm{1}−\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{1}−\frac{\mathrm{tan}\:\mathrm{45}°\left(\mathrm{1}−\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°\right)}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}−\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°\mathrm{tan}\:\mathrm{25}°} \\ $$$$=\mathrm{2} \\ $$$${similarly} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{21}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{24}°}\right)=\mathrm{2} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{22}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{23}°}\right)=\mathrm{2} \\ $$$$\Rightarrow\underset{{i}=\mathrm{0}} {\overset{\mathrm{5}} {\prod}}\left(\mathrm{1}−\mathrm{cot}\:\left(\mathrm{20}+{i}\right)\right) \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{20}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{21}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{22}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{23}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{24}°}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{25}°}\right) \\ $$$$=\mathrm{2}×\mathrm{2}×\mathrm{2} \\ $$$$=\mathrm{8} \\ $$
