Question Number 142708 by ajfour last updated on 05/Jun/21
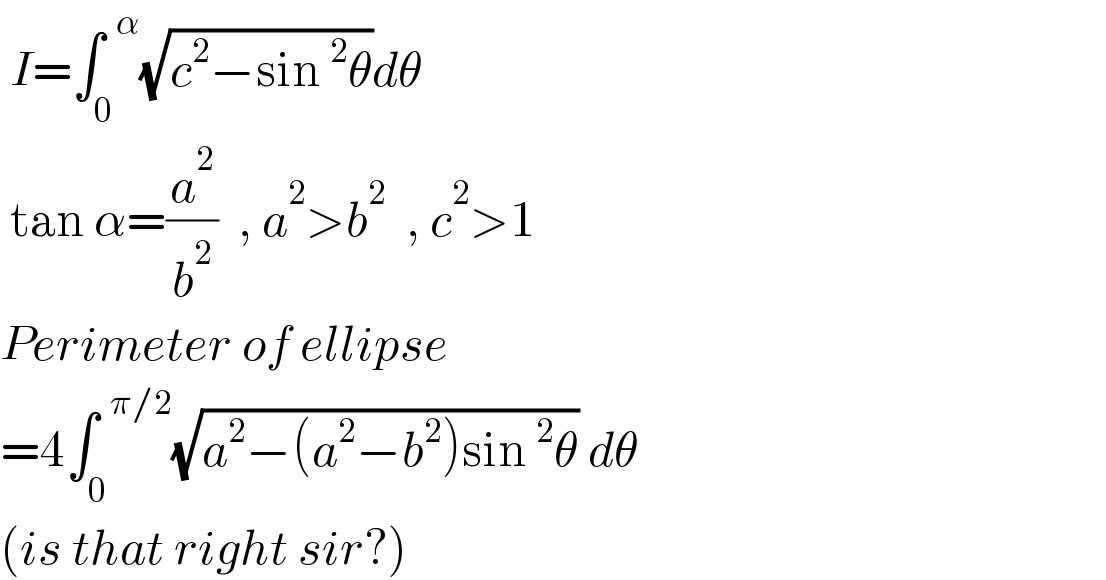
$$\:{I}=\int_{\mathrm{0}} ^{\:\:\alpha} \sqrt{{c}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \theta}{d}\theta \\ $$$$\:\mathrm{tan}\:\alpha=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\:,\:{a}^{\mathrm{2}} >{b}^{\mathrm{2}} \:\:,\:{c}^{\mathrm{2}} >\mathrm{1} \\ $$$${Perimeter}\:{of}\:{ellipse} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$\left({is}\:{that}\:{right}\:{sir}?\right) \\ $$
Answered by MJS_new last updated on 04/Jun/21
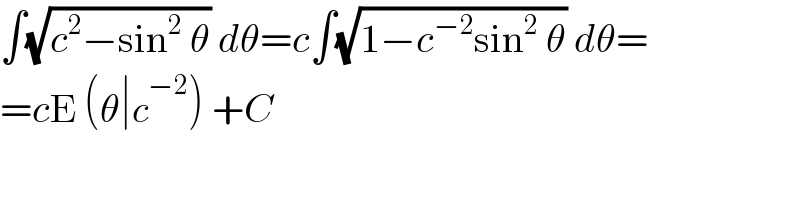
$$\int\sqrt{{c}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\theta}\:{d}\theta={c}\int\sqrt{\mathrm{1}−{c}^{−\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}\:{d}\theta= \\ $$$$={c}\mathrm{E}\:\left(\theta\mid{c}^{−\mathrm{2}} \right)\:+{C} \\ $$
Commented by ajfour last updated on 05/Jun/21
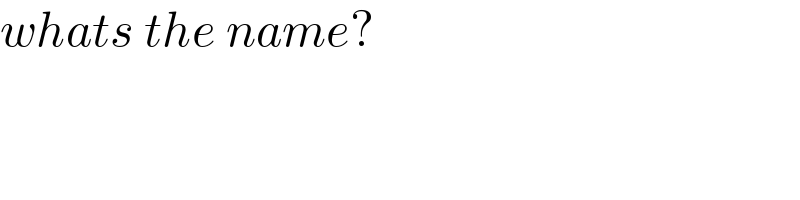
$${whats}\:{the}\:{name}? \\ $$
Commented by MJS_new last updated on 05/Jun/21

$$\mathrm{Incomplete}\:\mathrm{Elliptic}\:\mathrm{Integral}\:\mathrm{of}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{Kind} \\ $$
Commented by mohammad17 last updated on 05/Jun/21
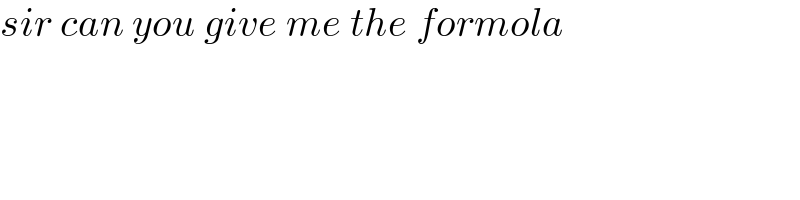
$${sir}\:{can}\:{you}\:{give}\:{me}\:{the}\:{formola} \\ $$
