Question Number 70602 by oyemi kemewari last updated on 06/Oct/19
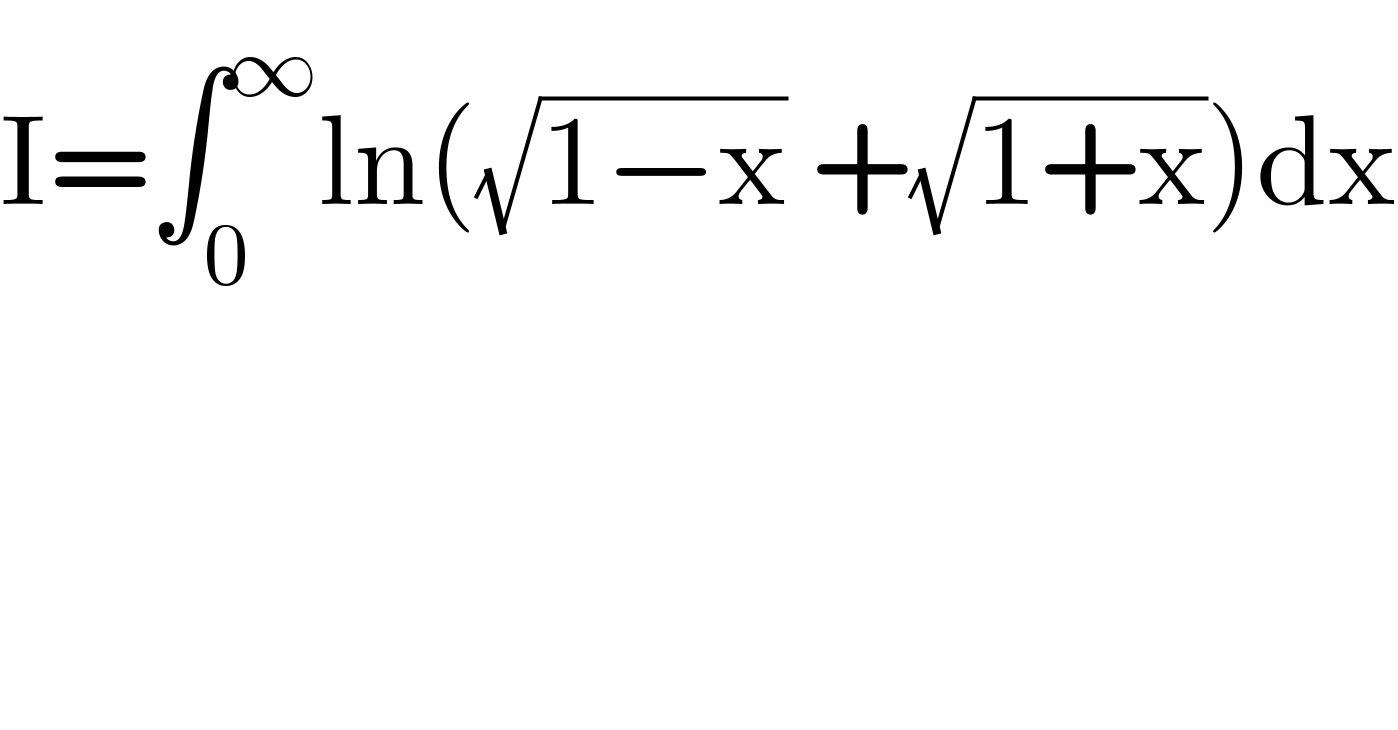
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{ln}\left(\sqrt{\mathrm{1}−\mathrm{x}}\:+\sqrt{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 06/Oct/19
![error in the question the function x→(√(1−x))+(√(1+x)) is defined on [−1,1]....!](https://www.tinkutara.com/question/Q70644.png)
$${error}\:{in}\:{the}\:{question}\:{the}\:{function}\:{x}\rightarrow\sqrt{\mathrm{1}−{x}}+\sqrt{\mathrm{1}+{x}}\:{is}\:{defined}\:{on} \\ $$$$\left[−\mathrm{1},\mathrm{1}\right]….! \\ $$
