Question Number 1085 by 123456 last updated on 10/Jun/15
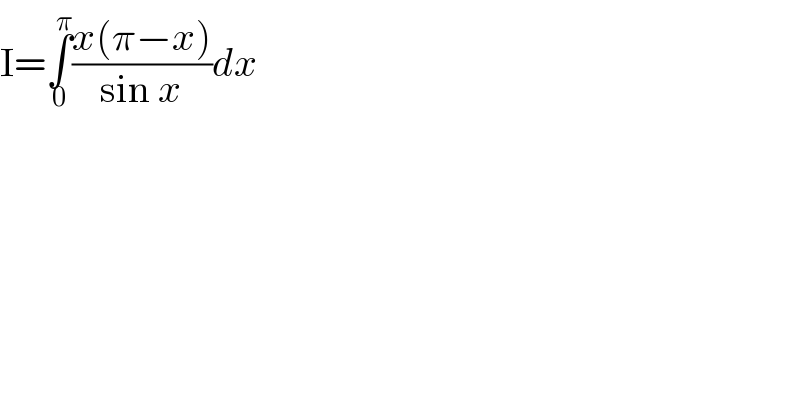
$$\mathrm{I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{x}\left(\pi−{x}\right)}{\mathrm{sin}\:{x}}{dx} \\ $$
Commented by 123456 last updated on 10/Jun/15
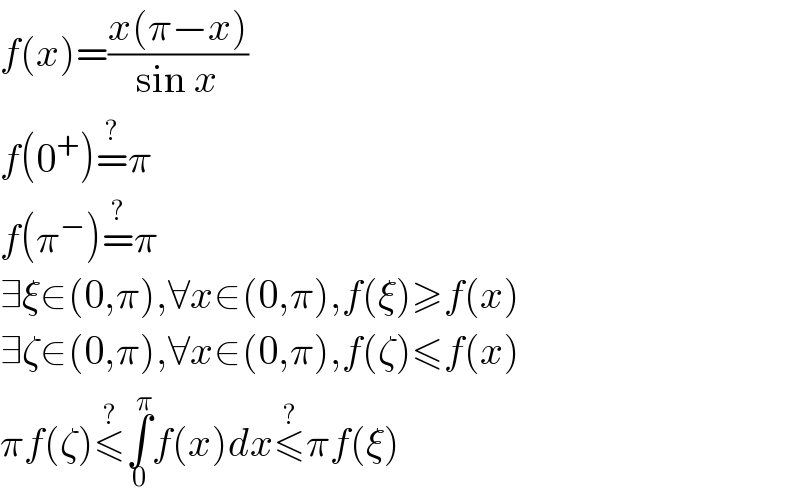
$${f}\left({x}\right)=\frac{{x}\left(\pi−{x}\right)}{\mathrm{sin}\:{x}} \\ $$$${f}\left(\mathrm{0}^{+} \right)\overset{?} {=}\pi \\ $$$${f}\left(\pi^{−} \right)\overset{?} {=}\pi \\ $$$$\exists\xi\in\left(\mathrm{0},\pi\right),\forall{x}\in\left(\mathrm{0},\pi\right),{f}\left(\xi\right)\geqslant{f}\left({x}\right) \\ $$$$\exists\zeta\in\left(\mathrm{0},\pi\right),\forall{x}\in\left(\mathrm{0},\pi\right),{f}\left(\zeta\right)\leqslant{f}\left({x}\right) \\ $$$$\pi{f}\left(\zeta\right)\overset{?} {\leqslant}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){dx}\overset{?} {\leqslant}\pi{f}\left(\xi\right) \\ $$
Commented by 123456 last updated on 10/Jun/15
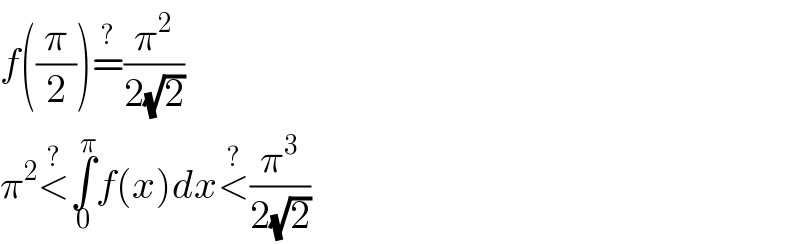
$${f}\left(\frac{\pi}{\mathrm{2}}\right)\overset{?} {=}\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\pi^{\mathrm{2}} \overset{?} {<}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){dx}\overset{?} {<}\frac{\pi^{\mathrm{3}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Commented by prakash jain last updated on 10/Jun/15

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}\left(\pi−{x}\right)}{\mathrm{sin}\:{x}}=\pi \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{x}\left(\pi−{x}\right)}{\mathrm{sin}\:{x}}=\pi \\ $$
