Question Number 141848 by iloveisrael last updated on 24/May/21
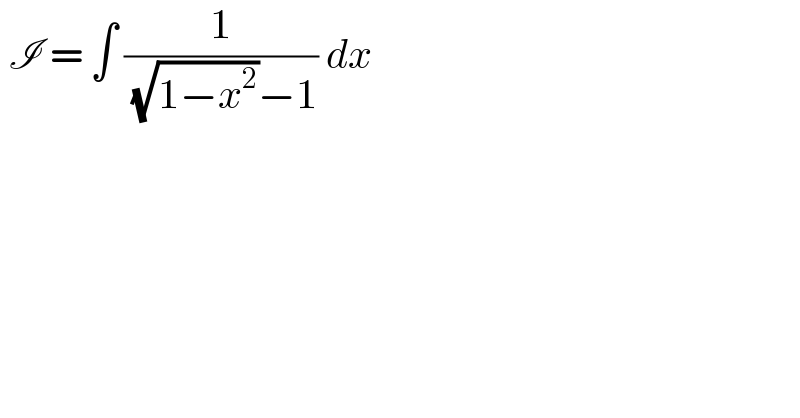
$$\:\mathscr{I}\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}}\:{dx}\: \\ $$
Answered by ArielVyny last updated on 24/May/21
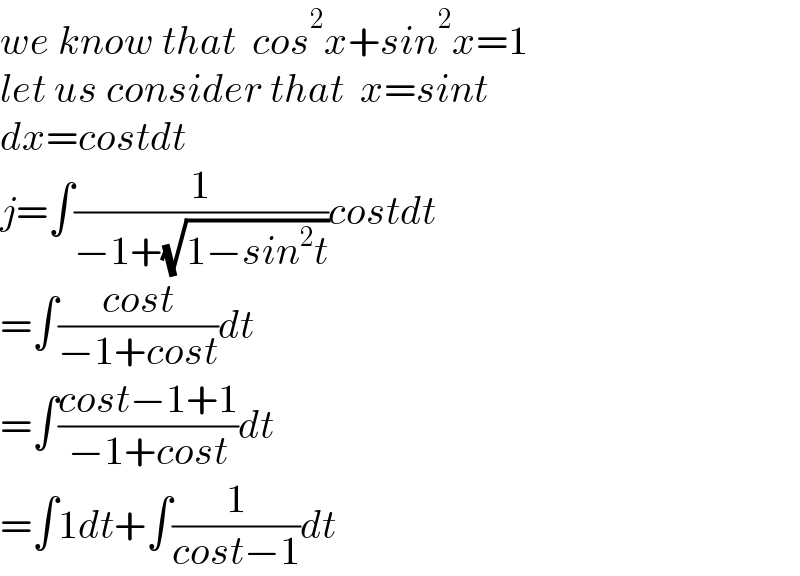
$${we}\:{know}\:{that}\:\:{cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$${let}\:{us}\:{consider}\:{that}\:\:{x}={sint} \\ $$$${dx}={costdt} \\ $$$${j}=\int\frac{\mathrm{1}}{−\mathrm{1}+\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {t}}}{costdt} \\ $$$$=\int\frac{{cost}}{−\mathrm{1}+{cost}}{dt} \\ $$$$=\int\frac{{cost}−\mathrm{1}+\mathrm{1}}{−\mathrm{1}+{cost}}{dt} \\ $$$$=\int\mathrm{1}{dt}+\int\frac{\mathrm{1}}{{cost}−\mathrm{1}}{dt} \\ $$
Answered by iloveisrael last updated on 24/May/21

$$\:\mathcal{I}\:=\:\int\:\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+\mathrm{1}}{−{x}^{\mathrm{2}} }\:{dx} \\ $$$${I}=−\int\:\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:{dx}\:−\int\:{x}^{−\mathrm{2}} \:{dx} \\ $$$${I}=\frac{\mathrm{1}}{{x}}−\int\:\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:{dx}\: \\ $$$${set}\:{x}\:=\:\mathrm{sin}\:{q}\:\Rightarrow{dx}\:=\:\mathrm{cos}\:{q}\:{dq} \\ $$$${I}=\frac{\mathrm{1}}{{x}}−\int\:\frac{\mathrm{cos}\:{q}}{\mathrm{sin}\:^{\mathrm{2}} }\:\left(\mathrm{cos}\:{q}\:{dq}\right) \\ $$$${I}=\frac{\mathrm{1}}{{x}}−\int\:\mathrm{cot}\:^{\mathrm{2}} {q}\:{dq}\: \\ $$$${I}=\frac{\mathrm{1}}{{x}}−\int\:\left(\mathrm{csc}\:^{\mathrm{2}} {q}−\mathrm{1}\right){dq} \\ $$$${I}=\frac{\mathrm{1}}{{x}}+{q}+\mathrm{cot}\:{q}\:+\:{c} \\ $$$${I}=\frac{\mathrm{1}}{{x}}+\mathrm{arcsin}\:{x}\:+\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+{c} \\ $$$${I}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+\:\mathrm{arcsin}\:{x}\:+\:{c}\: \\ $$
Answered by MJS_new last updated on 24/May/21
![∫(dx/( (√(1−x^2 ))−1))=−∫((1+(√(1−x^2 )))/x^2 )dx= [t=((1+(√(1−x^2 )))/x) → dx=−((x^2 (√(1−x^2 )))/(1+(√(1−x^2 ))))dt] =∫((t^2 −1)/(t^2 +1))dt=∫(1−(2/(t^2 +1)))dt=t−2arctan t = =((1+(√(1−x^2 )))/x)−2arctan ((1+(√(1−x^2 )))/x) +C](https://www.tinkutara.com/question/Q141883.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}}=−\int\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dt}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\int\left(\mathrm{1}−\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}={t}−\mathrm{2arctan}\:{t}\:= \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}−\mathrm{2arctan}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+{C} \\ $$
Answered by mathmax by abdo last updated on 24/May/21
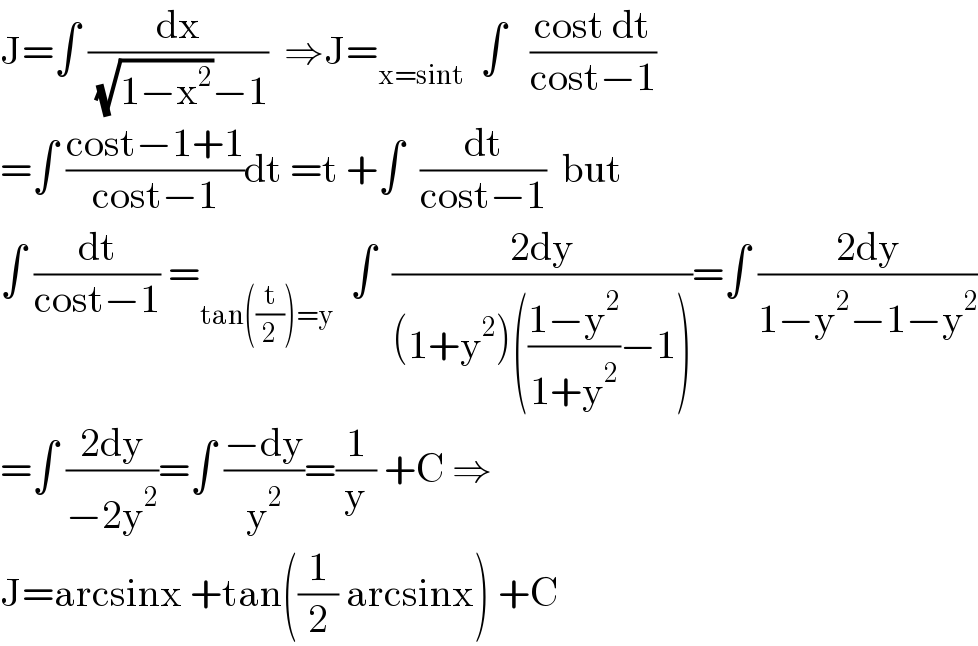
$$\mathrm{J}=\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }−\mathrm{1}}\:\:\Rightarrow\mathrm{J}=_{\mathrm{x}=\mathrm{sint}} \:\:\int\:\:\:\frac{\mathrm{cost}\:\mathrm{dt}}{\mathrm{cost}−\mathrm{1}} \\ $$$$=\int\:\frac{\mathrm{cost}−\mathrm{1}+\mathrm{1}}{\mathrm{cost}−\mathrm{1}}\mathrm{dt}\:=\mathrm{t}\:+\int\:\:\frac{\mathrm{dt}}{\mathrm{cost}−\mathrm{1}}\:\:\mathrm{but} \\ $$$$\int\:\frac{\mathrm{dt}}{\mathrm{cost}−\mathrm{1}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }−\mathrm{1}\right)}=\int\:\frac{\mathrm{2dy}}{\mathrm{1}−\mathrm{y}^{\mathrm{2}} −\mathrm{1}−\mathrm{y}^{\mathrm{2}} } \\ $$$$=\int\:\frac{\mathrm{2dy}}{−\mathrm{2y}^{\mathrm{2}} }=\int\:\frac{−\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{y}}\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{J}=\mathrm{arcsinx}\:+\mathrm{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arcsinx}\right)\:+\mathrm{C} \\ $$
